Product Description
115mm ZB Series Agricultural Machinery High Precision and Small Backlash Planetary Gearbox
Detailed Photos
Product Parameters
Note : It’s just the typical technical data for you reference, The specification such as voltage, speed, torque, shaft can be customized by your needs. Please contact us for more details. Thanks.
Company Profile
FAQ
Q: What’re your main products?
A: We currently produce Brushed Dc Motors, Brushed Dc Gear Motors, Planetary Dc Gear Motors, Brushless Dc Motors, Stepper motors, Ac Motors and High Precision Planetary Gear Box etc. You can check the specifications for above motors on our website and you can email us to recommend needed motors per your specification too.
Q: How to select a suitable motor?
A:If you have motor pictures or drawings to show us, or you have detailed specs like voltage, speed, torque, motor size, working mode of the motor, needed lifetime and noise level etc, please do not hesitate to let us know, then we can recommend suitable motor per your request accordingly.
Q: Do you have a customized service for your standard motors?
A: Yes, we can customize per your request for the voltage, speed, torque and shaft size/shape. If you need additional wires/cables soldered on the terminal or need to add connectors, or capacitors or EMC we can make it too.
Q: Do you have an individual design service for motors?
A: Yes, we would like to design motors individually for our customers, but it may need some mold developing cost and design charge.
Q: What’s your lead time?
A: Generally speaking, our regular standard product will need 15-30days, a bit longer for customized products. But we are very flexible on the lead time, it will depend on the specific orders.
Please contact us if you have detailed requests, thank you !
| Application: | Motor, Machinery |
|---|---|
| Function: | Speed Changing, Speed Reduction |
| Layout: | Cycloidal |
| Hardness: | Hardened Tooth Surface |
| Installation: | Vertical Type |
| Step: | Three-Step |
| Customization: |
Available
| Customized Request |
|---|

Condition Monitoring of Cyclone Gearboxes
Whether you’re considering using a cycloidal gearbox in your home, office, or garage, you’ll want to make sure it’s made of quality material. You also want to make sure it’s designed properly, so it won’t be damaged by vibrations.
Planetary gearboxes
Compared to cycloidal gearboxes, planetary gearboxes are lighter and more compact, but they lack the precision and durability of the former. They are better suited for applications with high torque or speed requirements. For this reason, they are usually used in robotics applications. But, cycloidal gearboxes are still better for some applications, including those involving shock loads.
There are many factors that affect the performance of gearboxes during production. One of these is the number of teeth. In the case of planetary gearboxes, the number of teeth increases with the number of planets. The number of teeth is reduced in cycloidal gearboxes, which results in higher transmission ratios. These gearboxes also have lower breakaway torques, which means that they can be controlled more easily by the user.
A cycloid gearbox is comprised of three main parts: the ring gear, the sun gear, and the input shaft. The ring gear is fixed in the gearbox, while the sun gear transmits the rotation to the planet gears. The input shaft transfers motion to the sun gear, which in turn transmits it to the output shaft. The output shaft has a larger torque than the input shaft.
Cycloid gears have better torsional stiffness, lower wear, and lower Hertzian contact stress. However, they are also larger in size and require highly accurate manufacturing. Cycloid gears can be more difficult to manufacture than involute gears, which require large amounts of precision.
Cycloid gears can offer transmission ratios up to 300:1, and they can do this in a small package. They also have lower wear and friction, which makes them ideal for applications that require a high transmission ratio.
Cycloid gearboxes are usually equipped with a backlash of about one angular minute. This backlash provides the precision and control necessary for accurate movement. They also provide low wear and shock load capacity.
Planetary gearboxes are available in single and two-stage designs, which increase in length as stages are added. In addition to the two stages, they can be equipped with an optional output bearing, which takes up mounting space. In some applications, a third stage is also available.
Involute gears
Generally, involute gears are more complex to manufacture than cycloidal gears. For example, an involute gear tooth profile has a single curve while a cycloidal gear tooth profile has two curves. In addition, the involute curve is not within the base circle.
The involute curve is a very important component of a gear tooth and it can significantly influence the quality of contact meshing between teeth. Various works have been done on the subject, mainly focusing on the operating principles. In addition, the most important characteristic of the double-enveloping cycloid drive is its double contact lines between the meshing tooth pairs.
Cycloid gears are more powerful, less noisy, and last longer than involute gears. They also require less manufacturing operations during production. However, cycloid gears are more expensive than involute gears. Involute gears are more commonly used in linear motions while cycloid gears are used for rotary motions.
Although cycloid gears are more technically advanced, involute gears have the superior quality and are more aesthetically pleasing. Cycloid gears are used in various industrial applications such as pumps and compressors. They are also widely used in the watch industry. Nevertheless, involute gears have not yet replaced cycloid gears in the watch industry.
The cycloid disc has a number of pins around its outer edge, while an involute gear has only a single curve for the teeth. In addition, cycloid gears have a more robust and reliable design. Involute gears, on the other hand, have a cheaper rack cutter and less expensive involute teeth.
The cycloid disc’s transmission accuracy is about 98.5%, while the ring gear’s transmission accuracy is about 96%. The cycloid disc’s rotational velocity has a magnitude of 3 rad/s. A small change in the center distance does not affect the transmission accuracy. However, rotational velocity fluctuation can affect the transmission accuracy.
Cycloid gears also have the cycloid gear disc’s rotational velocity. The disc has N lobes. However, the cycloid gear disc’s transmission accuracy is still not perfect. This is because of the large rotational angles between the lobes. This also makes it difficult to manufacture.
Vibrations
Using modern techniques for vibration diagnostics and data-driven methods, this article presents a new approach to condition monitoring of cycloidal gearboxes. This approach focuses on detecting the root cause of gearbox failure. The article aims to provide a unified approach to gear designers.
A cycloidal gearbox is a high-precision gearbox that is used in heavy-duty machines. It has a large reduction ratio, which makes it necessary to have a very large input speed. Cycloid gears have high accuracy, but they are susceptible to vibration issues. In this article, the authors describe how a cycloidal gearbox works and how vibrations are measured. They also show how this gearbox can be used to detect faults.
The gearbox is used in positioners, multi-axis robots, and heavy-duty machines. The main characteristics of this gearbox are the high accuracy, the overload capacity, and the large reduction ratio.
There is little documentation on vibrations and condition monitoring of cycloidal gearboxes. The authors describe their approach to the problem, using a cycloidal gearbox and a testing bench. Their approach involves measuring the frequency of the gearbox with different input speeds.
The results show a good separation between the healthy and damaged states. Fault frequencies show up in the lower orders of frequencies. Faults can be detected using binning, which eliminates the need for a tachometer. In addition, binning is combined with Principal Component Analysis to determine the state of the gearbox.
This method is compared to traditional techniques. In addition, the results show how binning can be used to calculate the defect frequencies of the bearings. It is also used to determine the frequencies of the components.
The signals from the test bench are acquired using four sensors. These sensors are medium sensitivity 100 mV/g accelerometers. The signals are then processed using different signal processing techniques. The results show that the vibration signals are correlated with the internal motion of the gearbox. This information is used to identify the internal frequency of the transmission.
The frequency analysis of vibration signals is performed in cyclostationary and noncyclostationary conditions. The signals are then analyzed to determine the magnitude of the gear meshing frequency.
Design
Using precision gearboxes, servomotors can now control heavy loads at high speed. Unlike cam indexing devices, cycloidal gears provide extremely accurate positioning and high torque. They also provide excellent torsional stiffness and shock load capacity.
Cycloid gears are specially designed to minimize vibration at high RPM. Unlike involute gears, they are not stacked, which reduces friction and forces experienced by each tooth. In addition, cycloidal gears have lower Hertzian contact stress.
Cycloid gears are often used in multi-axis robots for positioners. They can provide transmission ratios as high as 300:1 in a compact package. They are also used in first joints in heavy machines. However, they require extremely accurate manufacturing. They are also more difficult to produce than involute gears.
A cycloidal gearbox is a type of planetary gearbox. Cycloid gears are specially designed for high gear ratios. They also have the ability to provide a large reduction ratio in a single stage. They are increasingly used in first joints in heavy machines. They are also becoming more common in robotics.
In order to achieve a large reduction ratio, the input speed of the gear must be very high. Generally, the input speed is between 500 rpm and 4500 rpm. However, in some cases, the input speed may be lower.
A cycloid is formed by rolling a rolling circle on a base circle. The ratio between the rolling circle diameter and the base circle diameter determines the shape of the cycloid. A hypocycloid is formed by rolling primarily on the inside of the base circle, while an epicycloid is formed by rolling primarily on the outside of the base circle.
Cycloid gears have a very small backlash, which minimizes the forces experienced by each tooth. These gears also have a good torsional stiffness, low friction, and shock load capacity. They also provide the best positioning accuracy.
The cycloidal gearbox was designed and built at Radom University. The design was based on three different cycloidal gears. The first pair had the external profile at the nominal dimension, while the second pair had the profile minus tolerance. The load plate had threaded screw holes arranged 15 mm away from the center.

editor by CX 2023-10-22
China Hot selling ZD High Power Low Noise Brushless DC Gear Motor For Access Control System precision cycloidal gearbox
Product Description
ZD High Power Low Noise Brushless DC Gear Motor For Access Control System
Detailed Photos
Related BLDC Motors
Product Parameters
Main data:
1. Basic specification: DC24V, 60W, 2500RPM S1, B CLASS, IP20, IP40. OR12V, 48V. 250W. Customized products are welcome.
2. Rated torque of bare motor: 318mN. M, 229mNm
3. No-load noise of whole motor: <50dB, L=50cm
4. VE: AC66V, 1S, 5mA
5. Insulation resistance: >20MΩ 500V, >20MΩ 500V
6. Life: 2500H, 4000H
7. Ambient request: RoHS
8. Gear Ratio: 8.5, 12.5, 13
Company Profile
FAQ
Q: What’re your main products?
A: We currently produce Brushed Dc Motors, Brushed Dc Gear Motors, Planetary Dc Gear Motors, Brushless Dc Motors, Stepper motors, Ac Motors and High Precision Planetary Gear Box etc. You can check the specifications for above motors on our website and you can email us to recommend needed motors per your specification too.
Q: How to select a suitable motor?
A:If you have motor pictures or drawings to show us, or you have detailed specs like voltage, speed, torque, motor size, working mode of the motor, needed lifetime and noise level etc, please do not hesitate to let us know, then we can recommend suitable motor per your request accordingly.
Q: Do you have a customized service for your standard motors?
A: Yes, we can customize per your request for the voltage, speed, torque and shaft size/shape. If you need additional wires/cables soldered on the terminal or need to add connectors, or capacitors or EMC we can make it too.
Q: Do you have an individual design service for motors?
A: Yes, we would like to design motors individually for our customers, but it may need some mold developing cost and design charge.
Q: What’s your lead time?
A: Generally speaking, our regular standard product will need 15-30days, a bit longer for customized products. But we are very flexible on the lead time, it will depend on the specific orders.
Please contact us if you have detailed requests, thank you !
| Application: | Motor, Motorcycle, Machinery, Agricultural Machinery |
|---|---|
| Function: | Change Drive Torque, Speed Changing, Speed Reduction |
| Layout: | Cycloidal |
| Hardness: | Soft Tooth Surface |
| Installation: | Horizontal Type |
| Step: | Double-Step |
| Customization: |
Available
| Customized Request |
|---|

Developing a Mathematical Model of a Cyclone Gearbox
Compared to planetary gearboxes, cycloidal gearboxes are often seen as the ideal choice for a wide range of applications. They feature compact designs that are often low friction and high reduction ratios.
Low friction
Developing a mathematical model of a cycloidal gearbox was a challenge. The model was able to show the effects of a variety of geometric parameters on contact stresses. It was able to model stiction in all quadrants. It was able to show a clear correlation between the results from simulation and real-world measurements.
The model is based on a new approach that enables modeling stiction in all quadrants of a gearbox. It is also able to display non-zero current at standstill. Combined with a good simulation algorithm, the model can be used to improve the dynamic behaviour of a controlled system.
A cycloidal gearbox is a compact actuator used for industrial automation. This type of gearbox provides high gear ratios, low wear, and good torsional stiffness. In addition, it has good shock load capacity.
The model is based on cycloidal discs that engage with pins on a stationary ring gear. The resulting friction function occurs when the rotor begins to rotate. It also occurs when the rotor reverses its rotation. The model has two curves, one for motor and one for generator mode.
The trochoidal profile on the cycloidal disc’s periphery is required for proper mating of the rotating parts. In addition, the profile should be defined accurately. This will allow an even distribution of contact forces.
The model was used to compare the relative performance of a cycloidal gearbox with that of an involute gearbox. This comparison indicates that the cycloidal gearbox can withstand more load than an involute gearbox. It is also able to last longer. It is also able to produce high gear ratios in a small space.
The model used is able to capture the exact geometry of the parts. It can also allow a better analysis of stresses.
Compact
Unlike helical gearing, compact cycloidal gearboxes can provide higher reduction ratios. They are more compact and less weighty. In addition, they provide better positioning accuracy.
Cycloid drives provide high torque and load capacity. They are also very efficient and robust. They are ideal for applications with heavy loads or shock loads. They also feature low backlash and high torsional stiffness. Cycloid gearboxes are available in a variety of designs.
Cycloid discs are mounted on an eccentric input shaft, which drives them around a stationary ring gear. The ring gear consists of many pins, and the cycloidal disc moves one lobe for every rotation of the input shaft. The output shaft contains roller pins, which rotate around holes in the cycloidal disc.
Cycloid drives are ideally suited to heavy loads and shock loads. They have high torsional stiffness and high reduction ratios, making them very efficient. Cycloid gearboxes have low backlash and high torque and are very compact.
Cycloid gearboxes are used for a wide variety of applications, including marine propulsion systems, CNC machining centers, medical technology, and manipulation robots. They are especially useful in applications with critical positioning accuracy, such as surgical positioning systems. Cycloid gearboxes feature extremely low hysteresis loss and low backlash over extended periods of use.
Cycloid discs are usually designed with a reduced cycloid diameter to minimize unbalance forces at high speeds. Cycloid drives also feature minimal backlash, a high reduction ratio, and excellent positioning accuracy. Cycloid gearboxes also have a long service life, compared to other gear drives. Cycloid drives are highly robust, and offer higher reduction ratios than helical gear drives.
Cycloid gearboxes have a low cost and are easy to print. CZPT gearboxes are available in a wide range of sizes and can produce high torque on the output axis.
High reduction ratio
Among the types of gearboxes available, a high reduction ratio cycloidal gearbox is a popular choice in the automation field. This gearbox is used in applications requiring precise output and high efficiency.
Cycloid gears can provide high torque and transmit it well. They have low friction and a small backlash. They are widely used in robotic joints. However, they require special tools to manufacture. Some have even been 3D printed.
A cycloidal gearbox is typically a three-stage structure that includes an input hub, an output hub, and two cycloidal gears that rotate around each other. The input hub mounts movable pins and rollers, while the output hub mounts a stationary ring gear.
The input shaft is driven by an eccentric bearing. The disc is then pushed against the ring gear, which causes it to rotate around the bearing. As the disc rotates, the pins on the ring gear drive the pins on the output shaft.
The input shaft rotates a maximum of nine revolutions, while the output shaft rotates three revolutions. This means that the input shaft has to rotate over eleven million times before the output shaft is able to rotate. The output shaft also rotates in the opposite direction of the input shaft.
In a two-stage differential cycloidal speed reducer, the input shaft uses a crank shaft design. The crank shaft connects the first and second cycloidal gears and actuates them simultaneously.
The first stage is a cycloidal disc, which is a gear tooth profile. It has n=7 lobes on its circumference. Each lobe moves around a reference pitch circle of pins. The disc then advances in 360deg steps.
The second stage is a cycloidal disc, also known as a “grinder gear”. The teeth on the outer gear are fewer than the teeth on the inner gear. This allows the gear to be geardown based on the number of teeth.
Kinematics
Various scholars have studied the kinematics of cycloidal gearbox. They have developed various approaches to modify the tooth profile of cycloidal gears. Some of these approaches involve changing the shape of the cycloidal disc, and changing the grinding wheel center position.
This paper describes a new approach to cycloid gear profile modification. It is based on a mathematical model and incorporates several important parameters such as pressure angle, backlash, and root clearance. The study offers a new way for modification design of cycloid gears in precision reducers for robots.
The pressure angle of a tooth profile is an intersegment angle between the normal direction and the velocity direction at a meshing point. The pressure angle distribution is important for determining force transmission performance of gear teeth in meshing. The distribution trend can be obtained by calculating the equation (5).
The mathematical model for modification of the tooth profile can be obtained by establishing the relationship between the pressure angle distribution and the modification function. The dependent variable is the modification DL and the independent variable is the pressure angle a.
The position of the reference point A is a major consideration in the modification design. It ensures the force transmission performance of the meshing segment is optimal. It is determined by the smallest profile pressure angle. The position is also dependent on the type of gear that is being modified. It is also influenced by the tooth backlash.
The mathematical model governing the pressure angle distribution is developed with DL=f(a). It is a piecewise function that determines the pressure angle distribution of a tooth profile. It can also be expressed as DL=ph.
The pressure angle of a tooth is also an angle between the common normal direction at the meshing point and the rotation velocity direction of the cycloid gear.
Planetary gearboxes vs cycloidal gearboxes
Generally, there are two types of gearboxes that are used for motion control applications: cycloidal gearbox and planetary gearbox. Cycloid gearboxes are used for high-frequency motions, while planetary gearboxes are suitable for low-speed applications. Both are highly accurate and precise gearboxes that are capable of handling heavy loads at high cycle rates. But they have different advantages and disadvantages. So, engineers need to determine which type of gearbox is best suited for their application.
Cycloid gearboxes are commonly used in industrial automation. They provide excellent performance with ratios as low as 10:1. They offer a more compact design, higher torque density and greater overload protection. They also require less space and are less expensive than planetary gearboxes.
On the other hand, planetary gearboxes are lightweight and offer a higher torque density. They are also capable of handling higher ratios. They have a longer life span and are more precise and durable. They can be found in a variety of styles, including square-framed, round-framed and double-frame designs. They offer a wide range of torque and speed capabilities and are used for numerous applications.
Cycloid gearboxes can be manufactured with different types of cycloidal cams, including single or compound cycloidal cams. Cycloid cams are cylindrical elements that have cam followers that rotate in an eccentric fashion. The cam followers act like teeth on the internal gear. Cycloid cams are a simple concept, but they have numerous advantages. They have a low backlash over extended periods of time, allowing for more accurate positioning. They also have internal compressive stresses and an overlap factor between the rolling elements.
Planetary gearboxes are characterized by three basic force-transmitting elements: ring gear, sun gear, and planet gear. They are generally two-stage gearboxes. The sun gear is attached to the input shaft, which in turn is attached to the servomotor. The ring gear turns the sun gear and the planet gear turns the output shaft.

editor by CX 2023-10-21
China OEM China Manufacturer Wholesale High Precision Worm Gear Speed Reducer and Robot Gearbox cycloidal drive gear ratio
Product Description
Product Description
China Manufacturer Wholesale high precision Worm Gear Speed Reducer and robot gearbox
HangZhou Fubao Electromechanical Technology Co., Ltd.WF series Speed Reducer and robot gearbox for 5 axis machining center developed and manufactured by WEITENSTAN together with German and ZheJiang technicians for many years.
High precision miniature cycloidal gearbox has the characteristics of smaller, ultra-thin, lightweight and high rigidity, anti-overload and high torque. With good deceleration performance, smooth operation and accurate positioning can be achieved. Integrated design, can be directly connected with the motor, to achieve high precision, high rigidity, high durability and other advantages. It is designed for high speed ratio, high geometric accuracy, low motion loss, large torque capacity and high stiffness applications. The compact design (minimum OD ≈40mm, currently the world’s smallest precision cycloidal pin-wheel reducer) allows it to be installed in limited Spaces.
The design of WEITENSTAN high-precision reducers is based on a new reduction principle and newly developed radial and axial output bearings. The result is a new generation of power transmission systems. The new drive concept allows WEITENSTAN gear units to be used directly in the gears of robot joints, rotary tables and various transport systems.
WEITENSTAN high-precision reducers are designed for applications requiring large speed ratios, high precision, low-loss motion, high torque capacity, and high rigidity. At the same time, they are compact in design, can be installed in limited spaces, and have small inertia.
Reducer drawings
Detailed Photos
Product Advantage
China Manufacturer Wholesale high precision Worm Gear Speed Reducer and robot gearbox
advantages:
1, fine precision cycloidal structure
Ultra flat shape is achieved through differential reduction mechanism and thin cross roller bearing, contributing to the compact size of the equipment. The combination of small size and unmatched superior parameters achieves the best combination of performance, price and size (high cost performance).
2. Excellent accuracy (transmission loss ≤1 arcmin)
Through the complex meshing of precision cycloid gear and high precision roller pin, higher transmission accuracy is achieved while maintaining small size and high speed ratio.
3, high rigidity
Increase the mesh rate to disperse the load, so the rigidity is high.
4. High overload capacity
It maintains trouble-free operation under abnormally low noise and vibration conditions while ensuring excellent overturning and torsional stiffness parameters. Integrated axial radial cross roller bearings, high load capacity and overload capacity of the reducer, can ensure users to provide a variety of temperature range of applications.
5, the motor installation is simple
Electromechanical integration design, can be directly connected with the motor, any brand of motor can be installed directly, without adding any device.
6. Maintenance free
Seal grease to achieve maintenance free. No refueling, no mounting direction restrictions.
7, stable performance
The manufacturing process of high wear-resistant materials and high precision parts has been certified by ISO9000 quality system, which guarantees the reliable operation of the reducer.
Product Classification
WF Series
High Precision Miniature Reducer
WF series is a high precision micro cycloidal reducer with flange, which has a wide range of applications. This series of reducers includes precise reduction mechanisms and radial – axial roller bearings. The unique design allows load to act directly on the output flange or housing without additional bearings. WF series reducer is characterized by module design, can be installed through the flange motor and reducer, belongs to the motor directly connected reducer.
WFH Series
High Precision Miniature Reducer
WFH series is a hollow form of high precision miniature cycloidal reducer, wire, compressed air pipeline, drive shaft can be through the hollow shaft, non-motor direct connection type reducer. The WFH series is fully sealed, full of grease and includes precise deceleration mechanism and radial – axial roller bearings. The unique design allows load to be acted directly on the output flange or housing without additional bearings.
WR Series
high-precision corner reducer
The WR series is a flange output corner reducer. Like the WF and WFH series, it is a high-precision reducer (backlash less than 1 arc.min), and the level 2 can also be within 1 arc.min, which is higher than other types. Corner type reducer. It can replace the harmonic drive reducer, and its life and rigidity are more than 3 times that of the harmonic.
Product Parameters
| Size | reduction ratio | Rated output moment | Allowable torque of start and stop | Instantaneous allowable moment | Rated input speed | Maximum input speed | Tilt stiffness | Torsional stiffness | No-load starting torque | Transmission accuracy | Error accuracy | Moment of inertia | Weight | |
| Axis rotation | Shell rotation | Nm | Nm | Nm | rpm | rpm | Nm/arcmin | Nm/arcmin | Nm | arcmin | arcmin | kg-m² | kg | |
| WF07 | 21 | 20 | 15 | 30 | 45 | 3000 | 6000 | 6 | 1.1 | 0.12 | P1≤±1 P2≤±3 | P1≤±1 P2≤±3 | 0.52 | 0.42 |
| 41 | 40 | 0.11 | 0.47 | |||||||||||
| WF17 | 21 | 20 | 50 | 100 | 150 | 3000 | 6000 | 28 | 6 | 0.21 | P1≤±1 P2≤±3 | P1≤±1 P2≤±3 | 0.88 | 0.85 |
| 41 | 40 | 0.18 | 0.72 | |||||||||||
| 61 | 60 | 0.14 | 0.69 | |||||||||||
| WF25 | 21 | 20 | 110 | 220 | 330 | 3000 | 5500 | 131 | 24 | 0.47 | P1≤±1 P2≤±3 | P1≤±1 P2≤±3 | 6.12 | 2 |
| 31 | 30 | 0.41 | 5.67 | |||||||||||
| 41 | 40 | 0.38 | 4.9 | |||||||||||
| 51 | 50 | 0.35 | 4.56 | |||||||||||
| 81 | 80 | 0.31 | 4.25 | |||||||||||
| WF32 | 25 | 24 | 190 | 380 | 570 | 3000 | 4500 | 240 | 35 | 1.15 | P1≤±1 P2≤±3 | P1≤±1 P2≤±3 | 11 | 4.2 |
| 31 | 30 | 1.1 | 10.8 | |||||||||||
| 51 | 50 | 0.77 | 9.35 | |||||||||||
| 81 | 80 | 0.74 | 8.32 | |||||||||||
| 101 | 100 | 0.6 | 7.7 | |||||||||||
| WF40 | 25 | 24 | 320 | 640 | 960 | 3000 | 4000 | 377 | 50 | 1.35 | P1≤±1 P2≤±3 | P1≤±1 P2≤±3 | 13.2 | 6.6 |
| 31 | 30 | 1.32 | 12.96 | |||||||||||
| 51 | 50 | 0.92 | 11.22 | |||||||||||
| 81 | 80 | 0.81 | 9.84 | |||||||||||
| 121 | 120 | 0.72 | 8.4 | |||||||||||
Installation Instructions
Company Profile
Q: Speed reducer grease replacement time
A: When sealing appropriate amount of grease and running reducer, the standard replacement time is 20000 hours according to the aging condition of the grease. In addition, when the grease is stained or used in the surrounding temperature condition (above 40ºC), please check the aging and fouling of the grease, and specify the replacement time.
Q: Delivery time
A: Fubao has 2000+ production base, daily output of 1000+ units, standard models within 7 days of delivery.
Q: Reducer selection
A: Fubao provides professional product selection guidance, with higher product matching degree, higher cost performance and higher utilization rate.
Q: Application range of reducer
A: Fubao has a professional research and development team, complete category design, can match any stepping motor, servo motor, more accurate matching.
|
Shipping Cost:
Estimated freight per unit. |
To be negotiated |
|---|
| Application: | Motor, Machinery, Agricultural Machinery |
|---|---|
| Hardness: | Hardened Tooth Surface |
| Installation: | Horizontal Type |
| Customization: |
Available
| Customized Request |
|---|

Developing a Mathematical Model of a Cyclone Gearbox
Compared to planetary gearboxes, cycloidal gearboxes are often seen as the ideal choice for a wide range of applications. They feature compact designs that are often low friction and high reduction ratios.
Low friction
Developing a mathematical model of a cycloidal gearbox was a challenge. The model was able to show the effects of a variety of geometric parameters on contact stresses. It was able to model stiction in all quadrants. It was able to show a clear correlation between the results from simulation and real-world measurements.
The model is based on a new approach that enables modeling stiction in all quadrants of a gearbox. It is also able to display non-zero current at standstill. Combined with a good simulation algorithm, the model can be used to improve the dynamic behaviour of a controlled system.
A cycloidal gearbox is a compact actuator used for industrial automation. This type of gearbox provides high gear ratios, low wear, and good torsional stiffness. In addition, it has good shock load capacity.
The model is based on cycloidal discs that engage with pins on a stationary ring gear. The resulting friction function occurs when the rotor begins to rotate. It also occurs when the rotor reverses its rotation. The model has two curves, one for motor and one for generator mode.
The trochoidal profile on the cycloidal disc’s periphery is required for proper mating of the rotating parts. In addition, the profile should be defined accurately. This will allow an even distribution of contact forces.
The model was used to compare the relative performance of a cycloidal gearbox with that of an involute gearbox. This comparison indicates that the cycloidal gearbox can withstand more load than an involute gearbox. It is also able to last longer. It is also able to produce high gear ratios in a small space.
The model used is able to capture the exact geometry of the parts. It can also allow a better analysis of stresses.
Compact
Unlike helical gearing, compact cycloidal gearboxes can provide higher reduction ratios. They are more compact and less weighty. In addition, they provide better positioning accuracy.
Cycloid drives provide high torque and load capacity. They are also very efficient and robust. They are ideal for applications with heavy loads or shock loads. They also feature low backlash and high torsional stiffness. Cycloid gearboxes are available in a variety of designs.
Cycloid discs are mounted on an eccentric input shaft, which drives them around a stationary ring gear. The ring gear consists of many pins, and the cycloidal disc moves one lobe for every rotation of the input shaft. The output shaft contains roller pins, which rotate around holes in the cycloidal disc.
Cycloid drives are ideally suited to heavy loads and shock loads. They have high torsional stiffness and high reduction ratios, making them very efficient. Cycloid gearboxes have low backlash and high torque and are very compact.
Cycloid gearboxes are used for a wide variety of applications, including marine propulsion systems, CNC machining centers, medical technology, and manipulation robots. They are especially useful in applications with critical positioning accuracy, such as surgical positioning systems. Cycloid gearboxes feature extremely low hysteresis loss and low backlash over extended periods of use.
Cycloid discs are usually designed with a reduced cycloid diameter to minimize unbalance forces at high speeds. Cycloid drives also feature minimal backlash, a high reduction ratio, and excellent positioning accuracy. Cycloid gearboxes also have a long service life, compared to other gear drives. Cycloid drives are highly robust, and offer higher reduction ratios than helical gear drives.
Cycloid gearboxes have a low cost and are easy to print. CZPT gearboxes are available in a wide range of sizes and can produce high torque on the output axis.
High reduction ratio
Among the types of gearboxes available, a high reduction ratio cycloidal gearbox is a popular choice in the automation field. This gearbox is used in applications requiring precise output and high efficiency.
Cycloid gears can provide high torque and transmit it well. They have low friction and a small backlash. They are widely used in robotic joints. However, they require special tools to manufacture. Some have even been 3D printed.
A cycloidal gearbox is typically a three-stage structure that includes an input hub, an output hub, and two cycloidal gears that rotate around each other. The input hub mounts movable pins and rollers, while the output hub mounts a stationary ring gear.
The input shaft is driven by an eccentric bearing. The disc is then pushed against the ring gear, which causes it to rotate around the bearing. As the disc rotates, the pins on the ring gear drive the pins on the output shaft.
The input shaft rotates a maximum of nine revolutions, while the output shaft rotates three revolutions. This means that the input shaft has to rotate over eleven million times before the output shaft is able to rotate. The output shaft also rotates in the opposite direction of the input shaft.
In a two-stage differential cycloidal speed reducer, the input shaft uses a crank shaft design. The crank shaft connects the first and second cycloidal gears and actuates them simultaneously.
The first stage is a cycloidal disc, which is a gear tooth profile. It has n=7 lobes on its circumference. Each lobe moves around a reference pitch circle of pins. The disc then advances in 360deg steps.
The second stage is a cycloidal disc, also known as a “grinder gear”. The teeth on the outer gear are fewer than the teeth on the inner gear. This allows the gear to be geardown based on the number of teeth.
Kinematics
Various scholars have studied the kinematics of cycloidal gearbox. They have developed various approaches to modify the tooth profile of cycloidal gears. Some of these approaches involve changing the shape of the cycloidal disc, and changing the grinding wheel center position.
This paper describes a new approach to cycloid gear profile modification. It is based on a mathematical model and incorporates several important parameters such as pressure angle, backlash, and root clearance. The study offers a new way for modification design of cycloid gears in precision reducers for robots.
The pressure angle of a tooth profile is an intersegment angle between the normal direction and the velocity direction at a meshing point. The pressure angle distribution is important for determining force transmission performance of gear teeth in meshing. The distribution trend can be obtained by calculating the equation (5).
The mathematical model for modification of the tooth profile can be obtained by establishing the relationship between the pressure angle distribution and the modification function. The dependent variable is the modification DL and the independent variable is the pressure angle a.
The position of the reference point A is a major consideration in the modification design. It ensures the force transmission performance of the meshing segment is optimal. It is determined by the smallest profile pressure angle. The position is also dependent on the type of gear that is being modified. It is also influenced by the tooth backlash.
The mathematical model governing the pressure angle distribution is developed with DL=f(a). It is a piecewise function that determines the pressure angle distribution of a tooth profile. It can also be expressed as DL=ph.
The pressure angle of a tooth is also an angle between the common normal direction at the meshing point and the rotation velocity direction of the cycloid gear.
Planetary gearboxes vs cycloidal gearboxes
Generally, there are two types of gearboxes that are used for motion control applications: cycloidal gearbox and planetary gearbox. Cycloid gearboxes are used for high-frequency motions, while planetary gearboxes are suitable for low-speed applications. Both are highly accurate and precise gearboxes that are capable of handling heavy loads at high cycle rates. But they have different advantages and disadvantages. So, engineers need to determine which type of gearbox is best suited for their application.
Cycloid gearboxes are commonly used in industrial automation. They provide excellent performance with ratios as low as 10:1. They offer a more compact design, higher torque density and greater overload protection. They also require less space and are less expensive than planetary gearboxes.
On the other hand, planetary gearboxes are lightweight and offer a higher torque density. They are also capable of handling higher ratios. They have a longer life span and are more precise and durable. They can be found in a variety of styles, including square-framed, round-framed and double-frame designs. They offer a wide range of torque and speed capabilities and are used for numerous applications.
Cycloid gearboxes can be manufactured with different types of cycloidal cams, including single or compound cycloidal cams. Cycloid cams are cylindrical elements that have cam followers that rotate in an eccentric fashion. The cam followers act like teeth on the internal gear. Cycloid cams are a simple concept, but they have numerous advantages. They have a low backlash over extended periods of time, allowing for more accurate positioning. They also have internal compressive stresses and an overlap factor between the rolling elements.
Planetary gearboxes are characterized by three basic force-transmitting elements: ring gear, sun gear, and planet gear. They are generally two-stage gearboxes. The sun gear is attached to the input shaft, which in turn is attached to the servomotor. The ring gear turns the sun gear and the planet gear turns the output shaft.

editor by CX 2023-06-05
China factory High Precision Low Backlash Helical Gear Planetary Electric AC Geared Reducer Precision Planetary Gearbox for Servo Motor supplier
Product Description
TaiBang Motor Industry Group Co., Ltd.
The main products is induction motor, reversible motor, DC brush gear motor, DC brushless gear motor, CH/CV big gear motors, Planetary gear motor ,Worm gear motor etc, which used widely in various fields of manufacturing pipelining, transportation, food, medicine, printing, fabric, packing, office, apparatus, entertainment etc, and is the preferred and matched product for automatic machine.
Model Instruction
GB090-10-P2
| GB | 090 | 571 | P2 |
| Reducer Series Code | External Diameter | Reduction Ratio | Reducer Backlash |
| GB:High Precision Square Flange Output
GBR:High Precision Right Angle Square Flange Output GE:High Precision Round Flange Output GER:High Precision Right Round Flange Output |
050:ø50mm 070:ø70mm 090:ø90mm 120:ø120mm 155:ø155mm 205:ø205mm 235:ø235mm 042:42x42mm 060:60x60mm 090:90x90mm 115:115x115mm 142:142x142mm 180:180x180mm 220:220x220mm |
571 means 1:10 | P0:High Precision Backlash
P1:Precison Backlash P2:Standard Backlash |
Main Technical Performance
| Item | Number of stage | Reduction Ratio | GB042 | GB060 | GB060A | GB090 | GB090A | GB115 | GB142 | GB180 | GB220 |
| Rotary Inertia | 1 | 3 | 0.03 | 0.16 | 0.61 | 3.25 | 9.21 | 28.98 | 69.61 | ||
| 4 | 0.03 | 0.14 | 0.48 | 2.74 | 7.54 | 23.67 | 54.37 | ||||
| 5 | 0.03 | 0.13 | 0.47 | 2.71 | 7.42 | 23.29 | 53.27 | ||||
| 6 | 0.03 | 0.13 | 0.45 | 2.65 | 7.25 | 22.75 | 51.72 | ||||
| 7 | 0.03 | 0.13 | 0.45 | 2.62 | 7.14 | 22.48 | 50.97 | ||||
| 8 | 0.03 | 0.13 | 0.44 | 2.58 | 7.07 | 22.59 | 50.84 | ||||
| 9 | 0.03 | 0.13 | 0.44 | 2.57 | 7.04 | 22.53 | 50.63 | ||||
| 10 | 0.03 | 0.13 | 0.44 | 2.57 | 7.03 | 22.51 | 50.56 | ||||
| 2 | 15 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | |
| 20 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 25 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 30 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 35 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 40 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 45 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 50 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 | ||
| 60 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 | ||
| 70 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 | ||
| 80 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 | ||
| 90 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 | ||
| 100 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 |
| Item | Number of stage | GB042 | GB060 | GB060A | GB90 | GB090A | GB115 | GB142 | GB180 | GB220 | |
| Backlash(arcmin) | High Precision P0 | 1 | ≤1 | ≤1 | ≤1 | ≤1 | ≤1 | ≤1 | |||
| 2 | ≤3 | ≤3 | ≤3 | ≤3 | |||||||
| Precision P1 | 1 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | |
| 2 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ||
| Standard P2 | 1 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | |
| 2 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ||
| Torsional Rigidity(N.M/arcmin) | 1 | 3 | 7 | 7 | 14 | 14 | 25 | 50 | 145 | 225 | |
| 2 | 3 | 7 | 7 | 14 | 14 | 25 | 50 | 145 | 225 | ||
| Noise(dB) | 1,2 | ≤56 | ≤58 | ≤58 | ≤60 | ≤60 | ≤63 | ≤65 | ≤67 | ≤70 | |
| Rated input speed(rpm) | 1,2 | 5000 | 5000 | 5000 | 4000 | 4000 | 4000 | 3000 | 3000 | 2000 | |
| Max input speed(rpm) | 1,2 | 10000 | 10000 | 10000 | 8000 | 8000 | 8000 | 6000 | 6000 | 4000 | |
Noise test standard:Distance 1m,no load.Measured with an input speed 3000rpm
| Application: | Machinery, Agricultural Machinery |
|---|---|
| Function: | Distribution Power, Change Drive Torque, Change Drive Direction, Speed Reduction |
| Layout: | Cycloidal |
| Hardness: | Hardened Tooth Surface |
| Installation: | Vertical Type |
| Step: | Double-Step |
| Samples: |
US$ 50/Piece
1 Piece(Min.Order) | |
|---|
| Customization: |
Available
| Customized Request |
|---|

Cyclone Gearbox Vs Involute Gearbox
Whether you’re using a cycloidal gearbox or an involute gearbox for your application, there are a few things you should know. This article will highlight some of those things, including: cycloidal gearbox vs involute gearbox, weight, compressive force, precision, and torque density.
Compressive force
Several studies have been carried out to analyze the static characteristics of gears. In this article, the authors investigate the structural and kinematic principles of a cycloidal gearbox. The cycloidal gearbox is a gearbox that uses an eccentric bearing inside a rotating frame. It has no common pinion-gear pair, and is therefore ideal for a high reduction ratio.
The purpose of this paper is to investigate the stress distribution on a cycloidal disc. Various gear profiles are investigated in order to study the load distribution and dynamic effects.
Cycloidal gearboxes are subject to compression and backlash, which require the use of proper ratios for the bearing rate and the TSA. The paper also focuses on the kinematic principles of the reducer. In addition, the authors use standard analysis techniques for the shaft/gear and the cycloidal disc.
The authors previously worked on a rigid body dynamic simulation of a cycloidal reducer. The analysis used a trochoidal profile on the cycloidal disc periphery. The trochoidal profile is obtained from a manufacturing drawing and takes into account the tolerances.
The mesh density in the cycloidal disc captures the exact geometry of the parts. It provides accurate contact stresses.
The cycloidal disc consists of nine lobes, which move by one lobe per rotation of the drive shaft. However, when the disc is rotated around the pins, the cycloidal disc does not move around the center of gravity. Therefore, the cycloidal disc shares torque load with five outer rollers.
A low reduction ratio in a cycloidal gearbox results in a higher induced stress in the cycloidal disc. This is due to the bigger hole designed to reduce the material inside the disc.
Torque density
Several types of magnetic gearboxes have been studied. Some magnetic gearboxes have a higher torque density than others, but they are still not able to compete with the mechanical gearboxes.
A new high torque density cycloidal magnetic gearbox using Halbach rotors has been developed and is being tested. The design was validated by building a CPCyMG prototype. The results showed that the simulated slip torque was comparable to the experimental slip torque. The peak torque measured was a p3 = 14 spatial harmonic, and it corresponds to the active region torque density of 261.4 N*m/L.
This cycloidal gearbox also has a high gear ratio. It has been tested to achieve a peak torque of 147.8 Nm, which is more than double the torque density of the traditional cycloidal gearbox. The design incorporates a ferromagnetic back-support that provides mechanical fabrication support.
This cycloidal gearbox also shows how a small diameter can achieve a high torque density. It is designed with an axial length of 50mm. The radial deflection forces are not serious at this length. The design uses a small air gap to reduce the radial deflection forces, but it is not the only design option.
The trade-off design also has a high volumetric torque density. It has a smaller air gap and a higher mass torque density. It is feasible to make and mechanically strong. The design is also one of the most efficient in its class.
The helical gearing design is a newer technology that brings a higher level of precision to a cycloidal gearbox. It allows a servomotor to handle a heavy load at high cycle rates. It is also useful in applications that require smaller design envelopes.
Weight
Compared to planetary gearboxes, the weight of cycloidal gearboxes is not as significant. However, they do provide some advantages. One of the most significant features is their backlash-free operation, which helps them deliver smooth and precise movement.
In addition, they provide high efficiency, which means that servo motors can run at higher speeds. The best part is that they do not need to be stacked up in order to achieve a high ratio.
Another advantage of cycloidal gearboxes is that they are usually less expensive than planetary gearboxes. This means that they are suitable for the manufacturing industry and robotics. They are also suited for heavy-duty robots that require a robust gearbox.
They also provide a better reduction ratio. Cycloidal gears can achieve reduction ratios from 30:1 to 300:1, which is a huge improvement over planetary gears. However, there are few models available that provide a ratio below 30:1.
Cycloidal gears also offer more resistance to wear, which means that they can last longer than planetary gears. They are also more compact, which helps them achieve high ratios in a smaller space. The design of cycloidal gears also makes them less prone to backlash, which is one of the major shortcomings of planetary gearboxes.
In addition, cycloidal gears can also provide better positioning accuracy. In fact, this is one of the primary reasons for choosing cycloidal gears over planetary gears. This is because the cycloid disc rotates around a bearing independently of the input shaft.
Compared to planetary gearboxes, cycloidal gears are also much shorter. This means that they provide the best positioning accuracy. They are also 50% lighter, meaning that they have a smaller diameter.
Precision
Several experts have studied the cycloidal gearbox in precision reducers. Their research mainly focuses on the mathematical model and the method for precision evaluation of cycloidal gears.
The traditional modification design of cycloidal gears is mainly realized by setting various machining parameters and center position of the grinding wheel. But it has some disadvantages because of unstable meshing accuracy and uncontrollable tooth profile curve shape.
In this study, a new method of modification design of cycloidal gears is proposed. This method is based on the calculation of meshing backlash and pressure angle distribution. It can effectively pre-control the transmission accuracy of cycloid-pin gear. It can also ensure good meshing characteristics.
The proposed method can be applied in the manufacture of rotary vector reducers. It is also applicable in the precision reducer for robots.
The mathematical model for cycloidal gears can be established with the pressure angle a as a dependent variable. It is possible to calculate the pressure angle distribution and the profile pressure angle. It can also be expressed as DL=f(a). It can be applied in the design of precision reducers.
The study also considers the root clearance, the backlash of gear teeth and the profile angle. These factors have a direct effect on the transmission performance of cycloidal gear. It also indicates the higher motion accuracy and the smaller backlash. The modified profile can also reflect the smaller transmission error.
In addition, the proposed method is also based on the calculation of lost motion. It determines the angle of first tooth contacts. This angle is an important factor affecting the modification quality. The transmission error after the second cycloid method is the least.
Finally, a case study on the CZPT RV-35N gear pair is shown to prove the proposed method.
Involute gears vs cycloidal gears
Compared to involute gears, cycloidal gears have a lower noise, less friction, and last longer. However, they are more expensive. Cycloidal gears can be more difficult to manufacture. They may be less suitable for certain applications, including space manipulators and robotic joints.
The most common gear profile is the involute curve of a circle. This curve is formed by the endpoint of an imaginary taut string unwinding from the circle.
Another curve is the epicycloid curve. This curve is formed by the point rigidly attached to the circle rolling over another circle. This curve is difficult to produce and is much more expensive to produce than the involute curve.
The cycloid curve of a circle is also an example of the multi-cursor. This curve is generated by the locus of the point on the circle’s circumference.
The cycloid curve has the same diameter as the involute curve, but is tangentially curving along the circle’s diameter. This curve is also classified as ordinary. It has several other functions. The FE method was used to analyze the strain state of cycloidal speed reducers.
There are many other curves, but the involute curve is the most widely used gear profile. The involute curve of a circle is a spiraling curve traced by the endpoint of an imaginary tautstring.
Involute gears are a lot like a set of Lego blocks. They are a lot of fun to play with. They also have a lot of advantages. For example, they can handle center sifts better than cycloidal gears. They are also much easier to manufacture, so the cost of involute teeth is lower. However, they are obsolete.
Cycloidal gears are also more difficult to manufacture than involute gears. They have a convex surface, which leads to more wear. They also have a simpler shape than involute gears. They also have less teeth. They are used in rotary motions, such as in the rotors of screw compressors.

editor by CX 2023-04-26
China best 5r/m 0.4KW 190BX RVE Series High Precision Cycloidal Gearbox For Servo Motor cycloidal pin gear reducer
Merchandise Description
5r/m .4KW 190BX RVE Sequence High Precision Cycloidal Gearbox For Servo Motor
Design:190BX-RVE
Much more Code And Specification:
| E series | C sequence | ||||
| Code | Define dimension | General model | Code | Define dimension | The unique code |
| one hundred twenty | Φ122 | 6E | 10C | Φ145 | one hundred fifty |
| a hundred and fifty | Φ145 | 20E | 27C | Φ181 | one hundred eighty |
| a hundred ninety | Φ190 | 40E | 50C | Φ222 | 220 |
| 220 | Φ222 | 80E | 100C | Φ250 | 250 |
| 250 | Φ244 | 110E | 200C | Φ345 | 350 |
| 280 | Φ280 | 160E | 320C | Φ440 | 440 |
| 320 | Φ325 | 320E | 500C | Φ520 | 520 |
| 370 | Φ370 | 450E | |||
Gear ratio And Specification
| E Sequence | C Series | ||
| Code | Reduction Ratio | New code | Monomer reduction ratio |
| one hundred twenty | 43,53.5,59,79,103 | 10CBX | 27.00 |
| a hundred and fifty | eighty one,one hundred and five,121,141,161 | 27CBX | 36.57 |
| 190 | 81,a hundred and five,121,153 | 50CBX | 32.54 |
| 220 | eighty one,one hundred and one,121,153 | 100CBX | 36.75 |
| 250 | eighty one,111,161,one hundred seventy five.28 | 200CBX | 34.86 |
| 280 | eighty one,one zero one,129,145,171 | 320CBX | 35.sixty one |
| 320 | 81,a hundred and one,118.5,129,141,171,185 | 500CBX | 37.34 |
| 370 | 81,a hundred and one,118.5,129,154.8,171,192.4 | ||
| Note 1: E collection,these kinds of as by the shell(pin shell)output,the corresponding reduction ratio by one | |||
| Note 2: C collection equipment ratio refers to the motor installed in the casing of the reduction ratio,if put in on the output flange side,the corresponding reduction ratio by one | |||
Reducer variety code
REV: main bearing created-in E variety
RVC: hollow type
REA: with input flange E kind
RCA: with enter flange hollow sort
Software:
Company Data
FAQ
Q: What’re your major goods?
A: We currently make Brushed Dc Motors, Brushed Dc Equipment Motors, Planetary Dc Equipment Motors, Brushless Dc Motors, Stepper motors, Ac Motors and Substantial Precision Planetary Equipment Box and so forth. You can examine the requirements for previously mentioned motors on our website and you can electronic mail us to suggest needed motors for each your specification too.
Q: How to select a appropriate motor?
A:If you have motor images or drawings to show us, or you have comprehensive specs like voltage, pace, torque, motor dimension, working method of the motor, needed life time and sound stage etc, please do not hesitate to let us know, then we can advocate appropriate motor per your request appropriately.
Q: Do you have a customized support for your normal motors?
A: Yes, we can customize per your request for the voltage, pace, torque and shaft measurement/condition. If you require further wires/cables soldered on the terminal or require to add connectors, or capacitors or EMC we can make it also.
Q: Do you have an personal style support for motors?
A: Yes, we would like to design motors independently for our customers, but it might want some mildew developing price and layout demand.
Q: What is actually your lead time?
A: Usually talking, our standard regular product will need to have fifteen-30days, a bit more time for custom-made goods. But we are really versatile on the direct time, it will count on the certain orders.
Please contact us if you have comprehensive requests, thank you !
| Application: | Machinery, Robotic |
|---|---|
| Hardness: | Hardened Tooth Surface |
| Installation: | Vertical Type |
| Layout: | Coaxial |
| Gear Shape: | Cylindrical Gear |
| Step: | Double-Step |
| Customization: |
Available
| Customized Request |
|---|
Cyclone Gearbox Vs Involute Gearbox
Whether you’re using a cycloidal gearbox or an involute gearbox for your application, there are a few things you should know. This article will highlight some of those things, including: cycloidal gearbox vs involute gearbox, weight, compressive force, precision, and torque density.
Compressive force
Several studies have been carried out to analyze the static characteristics of gears. In this article, the authors investigate the structural and kinematic principles of a cycloidal gearbox. The cycloidal gearbox is a gearbox that uses an eccentric bearing inside a rotating frame. It has no common pinion-gear pair, and is therefore ideal for a high reduction ratio.
The purpose of this paper is to investigate the stress distribution on a cycloidal disc. Various gear profiles are investigated in order to study the load distribution and dynamic effects.
Cycloidal gearboxes are subject to compression and backlash, which require the use of proper ratios for the bearing rate and the TSA. The paper also focuses on the kinematic principles of the reducer. In addition, the authors use standard analysis techniques for the shaft/gear and the cycloidal disc.
The authors previously worked on a rigid body dynamic simulation of a cycloidal reducer. The analysis used a trochoidal profile on the cycloidal disc periphery. The trochoidal profile is obtained from a manufacturing drawing and takes into account the tolerances.
The mesh density in the cycloidal disc captures the exact geometry of the parts. It provides accurate contact stresses.
The cycloidal disc consists of nine lobes, which move by one lobe per rotation of the drive shaft. However, when the disc is rotated around the pins, the cycloidal disc does not move around the center of gravity. Therefore, the cycloidal disc shares torque load with five outer rollers.
A low reduction ratio in a cycloidal gearbox results in a higher induced stress in the cycloidal disc. This is due to the bigger hole designed to reduce the material inside the disc.
Torque density
Several types of magnetic gearboxes have been studied. Some magnetic gearboxes have a higher torque density than others, but they are still not able to compete with the mechanical gearboxes.
A new high torque density cycloidal magnetic gearbox using Halbach rotors has been developed and is being tested. The design was validated by building a CPCyMG prototype. The results showed that the simulated slip torque was comparable to the experimental slip torque. The peak torque measured was a p3 = 14 spatial harmonic, and it corresponds to the active region torque density of 261.4 N*m/L.
This cycloidal gearbox also has a high gear ratio. It has been tested to achieve a peak torque of 147.8 Nm, which is more than double the torque density of the traditional cycloidal gearbox. The design incorporates a ferromagnetic back-support that provides mechanical fabrication support.
This cycloidal gearbox also shows how a small diameter can achieve a high torque density. It is designed with an axial length of 50mm. The radial deflection forces are not serious at this length. The design uses a small air gap to reduce the radial deflection forces, but it is not the only design option.
The trade-off design also has a high volumetric torque density. It has a smaller air gap and a higher mass torque density. It is feasible to make and mechanically strong. The design is also one of the most efficient in its class.
The helical gearing design is a newer technology that brings a higher level of precision to a cycloidal gearbox. It allows a servomotor to handle a heavy load at high cycle rates. It is also useful in applications that require smaller design envelopes.
Weight
Compared to planetary gearboxes, the weight of cycloidal gearboxes is not as significant. However, they do provide some advantages. One of the most significant features is their backlash-free operation, which helps them deliver smooth and precise movement.
In addition, they provide high efficiency, which means that servo motors can run at higher speeds. The best part is that they do not need to be stacked up in order to achieve a high ratio.
Another advantage of cycloidal gearboxes is that they are usually less expensive than planetary gearboxes. This means that they are suitable for the manufacturing industry and robotics. They are also suited for heavy-duty robots that require a robust gearbox.
They also provide a better reduction ratio. Cycloidal gears can achieve reduction ratios from 30:1 to 300:1, which is a huge improvement over planetary gears. However, there are few models available that provide a ratio below 30:1.
Cycloidal gears also offer more resistance to wear, which means that they can last longer than planetary gears. They are also more compact, which helps them achieve high ratios in a smaller space. The design of cycloidal gears also makes them less prone to backlash, which is one of the major shortcomings of planetary gearboxes.
In addition, cycloidal gears can also provide better positioning accuracy. In fact, this is one of the primary reasons for choosing cycloidal gears over planetary gears. This is because the cycloid disc rotates around a bearing independently of the input shaft.
Compared to planetary gearboxes, cycloidal gears are also much shorter. This means that they provide the best positioning accuracy. They are also 50% lighter, meaning that they have a smaller diameter.
Precision
Several experts have studied the cycloidal gearbox in precision reducers. Their research mainly focuses on the mathematical model and the method for precision evaluation of cycloidal gears.
The traditional modification design of cycloidal gears is mainly realized by setting various machining parameters and center position of the grinding wheel. But it has some disadvantages because of unstable meshing accuracy and uncontrollable tooth profile curve shape.
In this study, a new method of modification design of cycloidal gears is proposed. This method is based on the calculation of meshing backlash and pressure angle distribution. It can effectively pre-control the transmission accuracy of cycloid-pin gear. It can also ensure good meshing characteristics.
The proposed method can be applied in the manufacture of rotary vector reducers. It is also applicable in the precision reducer for robots.
The mathematical model for cycloidal gears can be established with the pressure angle a as a dependent variable. It is possible to calculate the pressure angle distribution and the profile pressure angle. It can also be expressed as DL=f(a). It can be applied in the design of precision reducers.
The study also considers the root clearance, the backlash of gear teeth and the profile angle. These factors have a direct effect on the transmission performance of cycloidal gear. It also indicates the higher motion accuracy and the smaller backlash. The modified profile can also reflect the smaller transmission error.
In addition, the proposed method is also based on the calculation of lost motion. It determines the angle of first tooth contacts. This angle is an important factor affecting the modification quality. The transmission error after the second cycloid method is the least.
Finally, a case study on the CZPT RV-35N gear pair is shown to prove the proposed method.
Involute gears vs cycloidal gears
Compared to involute gears, cycloidal gears have a lower noise, less friction, and last longer. However, they are more expensive. Cycloidal gears can be more difficult to manufacture. They may be less suitable for certain applications, including space manipulators and robotic joints.
The most common gear profile is the involute curve of a circle. This curve is formed by the endpoint of an imaginary taut string unwinding from the circle.
Another curve is the epicycloid curve. This curve is formed by the point rigidly attached to the circle rolling over another circle. This curve is difficult to produce and is much more expensive to produce than the involute curve.
The cycloid curve of a circle is also an example of the multi-cursor. This curve is generated by the locus of the point on the circle’s circumference.
The cycloid curve has the same diameter as the involute curve, but is tangentially curving along the circle’s diameter. This curve is also classified as ordinary. It has several other functions. The FE method was used to analyze the strain state of cycloidal speed reducers.
There are many other curves, but the involute curve is the most widely used gear profile. The involute curve of a circle is a spiraling curve traced by the endpoint of an imaginary tautstring.
Involute gears are a lot like a set of Lego blocks. They are a lot of fun to play with. They also have a lot of advantages. For example, they can handle center sifts better than cycloidal gears. They are also much easier to manufacture, so the cost of involute teeth is lower. However, they are obsolete.
Cycloidal gears are also more difficult to manufacture than involute gears. They have a convex surface, which leads to more wear. They also have a simpler shape than involute gears. They also have less teeth. They are used in rotary motions, such as in the rotors of screw compressors.

editor by CX 2023-04-13
China 220BX REA Series High Precision Cycloidal Gearbox with Flange For Machinery cycloidal gear reducer design
Error:获取session失败,
| Application: | Machinery, Robotic |
|---|---|
| Hardness: | Hardened Tooth Surface |
| Installation: | Vertical Type |
| Layout: | Coaxial |
| Gear Shape: | Cylindrical Gear |
| Step: | Double-Step |
| Customization: |
Available
| Customized Request |
|---|
A Mathematical Model of a Cycloid Gearbox
Having a gearbox with a cycloidal rotor is an ideal design for a car or any other vehicle, as the cycloidal design can reduce the amplitude of vibration, which is a key component in car performance. Using a cycloidal gearbox is also a great way to reduce the amount of friction between the gears in the gearbox, which can help to reduce noise and wear and tear. A cycloidal gearbox is also a very efficient design for a vehicle that needs to perform under high loads, as the gearbox can be very robust against shock loads.
Basic design principles
cycloidal gearboxes are used for precision gearing applications. Cycloidal drives are compact and robust and offer lower backlash, torsional stiffness and a longer service life. They are also suitable for applications involving heavy loads.
Cycloidal drives are compact in size and provide very high reduction ratios. They are also very robust and can handle shock loads. Cycloidal drives are ideally suited to a wide range of drive technologies. Cycloidal gears have excellent torsional stiffness and can provide a transmission ratio of 300:1. They can also be used in applications where stacking multiple gear stages is not desired.
In order to achieve a high reduction ratio, cycloidal gears must be manufactured extremely accurately. Cycloidal gears have a curved tooth profile that removes shear forces at any point of contact. This provides a positive fit for the gear disc. This profile can be provided on a separate outer bushing or as an internal gear profile insert.
Cycloidal drives are used in marine propulsion systems, where the load plate rotates around the X and Y axis. The plate is anchored by a threaded screw hole arranged 15mm away from the center.
A secondary carrier body is used in a cycloidal gearbox to support the load plate. The secondary carrier body is composed of a mounting carrier body and a secondary carrier disc.
Low friction
Several studies have been conducted to understand the static problems of gears. In this paper, we discuss a mathematical model of a low friction cycloidal gearbox. This model is designed to calculate various parameters that affect the performance of the gearbox during production.
The model is based on a new approach that includes the stiction effect and the nonlinear friction characteristic. These parameters are not covered by the conventional rule of thumb.
The stiction effect is present when the speed direction is changed. During this time, the input torque is required to prevail over the stiction effect to generate movement. The model also enables us to calculate the magnitude of the stiction effect and its breakaway speed.
The most important thing is that the model can be used to improve the dynamic behavior of a controlled system. In this regard, the model has a high degree of accuracy. The model is tested in several quadrants of the gearbox to find the optimum stiction breakaway speed. The simulation results of the model show that this model is effective in predicting the efficiency of a low friction cycloidal gearbox.
In addition to the stiction model, we also studied the efficiency of a low friction cycloidal reducer. The reduction ratio of this gearbox was estimated from the formula. It is found that the ratio approaches negative infinity when the motor torque is close to zero Nm.
Compact
Unlike standard planetary gears, cycloidal gearboxes are compact, low friction and feature virtually zero backlash. They also offer high reduction ratios, high load capacity and high efficiency. These features make them a viable option for a variety of applications.
Cycloid disks are driven by an eccentric input shaft. They are then driven by a stationary ring gear. The ring gear rotates the cycloidal disk at a higher rate. The input shaft rotates nine times to complete a full rotation. The ring gear is designed to correct the dynamic imbalance.
CZPT cycloidal gearheads are designed for precision and stable operation. These reducers are robust and can handle large translocations. They also offer high overload protection. They are suitable for shock wave therapy. CZPT gearheads are also well suited for applications with critical positioning accuracy. They also require low assembly and design costs. They are designed for long service life and low hysteresis loss.
CZPT cycloidal reducers are used in a variety of industrial applications, including CNC machining centers, robot positioners and manipulators. They offer a unique design that can handle high forces on the output axis, and are especially suitable for large translocations. These gearheads are highly efficient, reducing costs, and are available in a variety of sizes. They are ideal for applications that require millimetre accuracy.
High reduction ratios
Compared to other gearboxes, cycloidal gearboxes offer high reduction ratios and small backlash. They are also less expensive. Cycloid gearboxes can be used in a variety of industries. They are suitable for robotic applications. They also have high efficiency and load capacity.
A cycloidal gearbox works by rotating a cycloidal disc. This disc contains holes that are bigger than the pins on the output shaft. When the disc is rotated, the output pins move in the holes to generate a steady output shaft rotation. This type of gearbox does not require stacking stages.
Cycloid gearboxes are usually shorter than planetary gearboxes. Moreover, they are more robust and can transmit higher torques.
Cycloid gearboxes have an eccentric cam that drives the cycloidal disc. The cycloidal disc advances in 360deg/pivot/roller steps. It also rotates in an eccentric pattern. It meshes with the ring-gear housing. It also engages the internal teeth of the ring-gear housing.
The number of lobes on the cycloidal disc is not sufficient to generate a good transmission ratio. In fact, the number of lobes must be less than the number of pins surrounding the cycloidal disc.
The cycloidal disc is rotated by an eccentric cam that extends from the base shaft. The cam also spins inside the cycloidal disc. The eccentric motion of the cam helps the cycloidal disc rotate around the pins of the ring-gear housing.
Reducing amplitude of the vibration
Various approaches to reducing amplitude of the vibration in a cycloidal gearbox have been studied. These approaches are based on the kinematic analysis of gearbox.
A cycloidal gearbox is a gearbox that consists of bearings, gears, and an eccentric bearing that drives a cycloidal disc. This gearbox has a high reduction ratio, which is achieved by a series of output shaft pins that drive the output shaft as the disc rotates.
The test bench used in the studies has four sensors. Each sensor acquires signals with different signal processing techniques. In addition, there is a tachometer that acquires variations in rotational velocity at the input side.
The kinematic study of the robotic gearbox was performed to understand the frequency of vibrations and to determine whether the gearbox is faulty. It was found that the gearbox is in healthy operation when the amplitude of the x and y is low. However, when the amplitude is high, it is indicative of a malfunctioning element.
The frequency analysis of vibration signals is performed for both cyclostationary and noncyclostationary conditions. The frequencies that are selected are those that appear in both types of conditions.
Robust against shock loads
Compared to traditional gearboxes, cycloidal gearboxes have significant benefits when it comes to shock loads. These include high shock-load capacity, high efficiency, reduced cost, lower weight, lower friction, and better positioning accuracy.
Cycloid gears can be used to replace traditional planetary gears in applications where inertia is important, such as the transportation of heavy loads. They have a lighter design and can be manufactured to a more compact size, which helps reduce cost and installation expense. Cycloid gears are also able to provide transmission ratios of up to 300:1 in a small package.
Cycloid gears are also suitable for applications where a long service life is essential. Their radial clamping ring reduces inertia by up to 39%. Cycloid gears have a torsional stiffness that is five times higher than that of conventional planetary gears.
Cycloid gearboxes can provide significant improvements in concrete mixers. They are a highly efficient design, which allows for important innovations. They are also ideal for servo applications, machine tools, and medical technology. They feature user-friendly screw connections, effective corrosion protection, and effective handling.
Cycloid gears are especially useful for applications with critical positioning accuracy. For example, in the control of large parabolic antennas, high shock load capacity is required to maintain accuracy. Cycloid gears can withstand shock loads up to 500% of their rated torque.
Inertial effects
Various studies have been conducted to investigate the static problems of gears. However, there is still a need for a proper model to investigate the dynamic behaviour of a controlled system. For this, a mathematical model of a cycloidal gearbox has been developed. The presented model is a simple model that can be used as the basis for a more complex mechanical model.
The mathematical model is based on the cycloidal gearbox’s mechanical construction and has a nonlinear friction characteristic. The model is able to reproduce the current peaks and breaks at standstill. It also considers the stiction effect. However, it does not cover backlash or torsional stiffness.
This model is used to calculate the torque generating current and the inertia of the motor. These values are then compared with the real system measurement. The results show that the simulation results are very close to the real system measurement.
Several parameters are considered in the model to improve its dynamic behaviour. These parameters are calculated from the harmonic drive system analysis. These are torque-generating current, inertia, and the contact forces of the rotating parts.
The model has a high level of accuracy and can be used for motor control. It is also able to reproduce the dynamic behaviour of a controlled system.

editor by CX 2023-04-11
China 220BX REA Series More Than 6000hr Life Time High Precision Cycloidal Gearbox with Flange cycloidal drive gear ratio
Product Description
220BX REA Collection A lot more Than 6000hr Existence Time High Precision Cycloidal Gearbox with Flange
Model:220BX-REA-35
Much more Code And Specification:
| E series | C sequence | ||||
| Code | Outline dimension | General design | Code | Define dimension | The original code |
| a hundred and twenty | Φ122 | 6E | 10C | Φ145 | 150 |
| one hundred fifty | Φ145 | 20E | 27C | Φ181 | 180 |
| 190 | Φ190 | 40E | 50C | Φ222 | 220 |
| 220 | Φ222 | 80E | 100C | Φ250 | 250 |
| 250 | Φ244 | 110E | 200C | Φ345 | 350 |
| 280 | Φ280 | 160E | 320C | Φ440 | 440 |
| 320 | Φ325 | 320E | 500C | Φ520 | 520 |
| 370 | Φ370 | 450E | |||
Equipment ratio And Specification
| E Series | C Sequence | ||
| Code | Reduction Ratio | New code | Monomer reduction ratio |
| a hundred and twenty | forty three,fifty three.5,59,seventy nine,103 | 10CBX | 27.00 |
| one hundred fifty | 81,a hundred and five,121,141,161 | 27CBX | 36.fifty seven |
| one hundred ninety | eighty one,one zero five,121,153 | 50CBX | 32.fifty four |
| 220 | eighty one,a hundred and one,121,153 | 100CBX | 36.75 |
| 250 | 81,111,161,a hundred seventy five.28 | 200CBX | 34.86 |
| 280 | 81,one zero one,129,145,171 | 320CBX | 35.61 |
| 320 | 81,a hundred and one,118.5,129,141,171,185 | 500CBX | 37.34 |
| 370 | eighty one,101,118.5,129,154.8,171,192.4 | ||
| Note 1: E series,these kinds of as by the shell(pin shell)output,the corresponding reduction ratio by one | |||
| Note 2: C series gear ratio refers to the motor installed in the casing of the reduction ratio,if put in on the output flange facet,the corresponding reduction ratio by 1 | |||
Reducer kind code
REV: main bearing created-in E sort
RVC: hollow type
REA: with enter flange E kind
RCA: with input flange hollow sort
Application:
Company Details
FAQ
Q: What’re your principal merchandise?
A: We at present create Brushed Dc Motors, Brushed Dc Gear Motors, Planetary Dc Gear Motors, Brushless Dc Motors, Stepper motors, Ac Motors and Large Precision Planetary Equipment Box and so on. You can examine the technical specs for previously mentioned motors on our website and you can e-mail us to advocate needed motors for every your specification too.
Q: How to choose a appropriate motor?
A:If you have motor pictures or drawings to show us, or you have thorough specs like voltage, pace, torque, motor dimensions, doing work method of the motor, necessary lifetime and noise stage and many others, remember to do not wait to let us know, then we can suggest appropriate motor for every your ask for accordingly.
Q: Do you have a tailored support for your normal motors?
A: Yes, we can customize per your ask for for the voltage, pace, torque and shaft dimensions/shape. If you need to have extra wires/cables soldered on the terminal or require to add connectors, or capacitors or EMC we can make it too.
Q: Do you have an personal style provider for motors?
A: Sure, we would like to design motors independently for our clients, but it could want some mould creating value and design demand.
Q: What is your lead time?
A: Normally talking, our standard common merchandise will want 15-30days, a little bit more time for custom-made items. But we are very adaptable on the lead time, it will rely on the specific orders.
You should get in touch with us if you have detailed requests, thank you !
| To Be Negotiated | 1 Piece (Min. Order) |
###
| Application: | Machinery, Robotic |
|---|---|
| Hardness: | Hardened Tooth Surface |
| Installation: | Vertical Type |
| Layout: | Coaxial |
| Gear Shape: | Cylindrical Gear |
| Step: | Double-Step |
###
| Customization: |
|---|
###
| E series | C series | ||||
| Code | Outline dimension | General model | Code | Outline dimension | The original code |
| 120 | Φ122 | 6E | 10C | Φ145 | 150 |
| 150 | Φ145 | 20E | 27C | Φ181 | 180 |
| 190 | Φ190 | 40E | 50C | Φ222 | 220 |
| 220 | Φ222 | 80E | 100C | Φ250 | 250 |
| 250 | Φ244 | 110E | 200C | Φ345 | 350 |
| 280 | Φ280 | 160E | 320C | Φ440 | 440 |
| 320 | Φ325 | 320E | 500C | Φ520 | 520 |
| 370 | Φ370 | 450E | |||
###
| E Series | C Series | ||
| Code | Reduction Ratio | New code | Monomer reduction ratio |
| 120 | 43,53.5,59,79,103 | 10CBX | 27.00 |
| 150 | 81,105,121,141,161 | 27CBX | 36.57 |
| 190 | 81,105,121,153 | 50CBX | 32.54 |
| 220 | 81,101,121,153 | 100CBX | 36.75 |
| 250 | 81,111,161,175.28 | 200CBX | 34.86 |
| 280 | 81,101,129,145,171 | 320CBX | 35.61 |
| 320 | 81,101,118.5,129,141,171,185 | 500CBX | 37.34 |
| 370 | 81,101,118.5,129,154.8,171,192.4 | ||
| Note 1: E series,such as by the shell(pin shell)output,the corresponding reduction ratio by 1 | |||
| Note 2: C series gear ratio refers to the motor installed in the casing of the reduction ratio,if installed on the output flange side,the corresponding reduction ratio by 1 | |||
| To Be Negotiated | 1 Piece (Min. Order) |
###
| Application: | Machinery, Robotic |
|---|---|
| Hardness: | Hardened Tooth Surface |
| Installation: | Vertical Type |
| Layout: | Coaxial |
| Gear Shape: | Cylindrical Gear |
| Step: | Double-Step |
###
| Customization: |
|---|
###
| E series | C series | ||||
| Code | Outline dimension | General model | Code | Outline dimension | The original code |
| 120 | Φ122 | 6E | 10C | Φ145 | 150 |
| 150 | Φ145 | 20E | 27C | Φ181 | 180 |
| 190 | Φ190 | 40E | 50C | Φ222 | 220 |
| 220 | Φ222 | 80E | 100C | Φ250 | 250 |
| 250 | Φ244 | 110E | 200C | Φ345 | 350 |
| 280 | Φ280 | 160E | 320C | Φ440 | 440 |
| 320 | Φ325 | 320E | 500C | Φ520 | 520 |
| 370 | Φ370 | 450E | |||
###
| E Series | C Series | ||
| Code | Reduction Ratio | New code | Monomer reduction ratio |
| 120 | 43,53.5,59,79,103 | 10CBX | 27.00 |
| 150 | 81,105,121,141,161 | 27CBX | 36.57 |
| 190 | 81,105,121,153 | 50CBX | 32.54 |
| 220 | 81,101,121,153 | 100CBX | 36.75 |
| 250 | 81,111,161,175.28 | 200CBX | 34.86 |
| 280 | 81,101,129,145,171 | 320CBX | 35.61 |
| 320 | 81,101,118.5,129,141,171,185 | 500CBX | 37.34 |
| 370 | 81,101,118.5,129,154.8,171,192.4 | ||
| Note 1: E series,such as by the shell(pin shell)output,the corresponding reduction ratio by 1 | |||
| Note 2: C series gear ratio refers to the motor installed in the casing of the reduction ratio,if installed on the output flange side,the corresponding reduction ratio by 1 | |||
Developing a Mathematical Model of a Cyclone Gearbox
Compared to planetary gearboxes, cycloidal gearboxes are often seen as the ideal choice for a wide range of applications. They feature compact designs that are often low friction and high reduction ratios.
Low friction
Developing a mathematical model of a cycloidal gearbox was a challenge. The model was able to show the effects of a variety of geometric parameters on contact stresses. It was able to model stiction in all quadrants. It was able to show a clear correlation between the results from simulation and real-world measurements.
The model is based on a new approach that enables modeling stiction in all quadrants of a gearbox. It is also able to display non-zero current at standstill. Combined with a good simulation algorithm, the model can be used to improve the dynamic behaviour of a controlled system.
A cycloidal gearbox is a compact actuator used for industrial automation. This type of gearbox provides high gear ratios, low wear, and good torsional stiffness. In addition, it has good shock load capacity.
The model is based on cycloidal discs that engage with pins on a stationary ring gear. The resulting friction function occurs when the rotor begins to rotate. It also occurs when the rotor reverses its rotation. The model has two curves, one for motor and one for generator mode.
The trochoidal profile on the cycloidal disc’s periphery is required for proper mating of the rotating parts. In addition, the profile should be defined accurately. This will allow an even distribution of contact forces.
The model was used to compare the relative performance of a cycloidal gearbox with that of an involute gearbox. This comparison indicates that the cycloidal gearbox can withstand more load than an involute gearbox. It is also able to last longer. It is also able to produce high gear ratios in a small space.
The model used is able to capture the exact geometry of the parts. It can also allow a better analysis of stresses.
Compact
Unlike helical gearing, compact cycloidal gearboxes can provide higher reduction ratios. They are more compact and less weighty. In addition, they provide better positioning accuracy.
Cycloid drives provide high torque and load capacity. They are also very efficient and robust. They are ideal for applications with heavy loads or shock loads. They also feature low backlash and high torsional stiffness. Cycloid gearboxes are available in a variety of designs.
Cycloid discs are mounted on an eccentric input shaft, which drives them around a stationary ring gear. The ring gear consists of many pins, and the cycloidal disc moves one lobe for every rotation of the input shaft. The output shaft contains roller pins, which rotate around holes in the cycloidal disc.
Cycloid drives are ideally suited to heavy loads and shock loads. They have high torsional stiffness and high reduction ratios, making them very efficient. Cycloid gearboxes have low backlash and high torque and are very compact.
Cycloid gearboxes are used for a wide variety of applications, including marine propulsion systems, CNC machining centers, medical technology, and manipulation robots. They are especially useful in applications with critical positioning accuracy, such as surgical positioning systems. Cycloid gearboxes feature extremely low hysteresis loss and low backlash over extended periods of use.
Cycloid discs are usually designed with a reduced cycloid diameter to minimize unbalance forces at high speeds. Cycloid drives also feature minimal backlash, a high reduction ratio, and excellent positioning accuracy. Cycloid gearboxes also have a long service life, compared to other gear drives. Cycloid drives are highly robust, and offer higher reduction ratios than helical gear drives.
Cycloid gearboxes have a low cost and are easy to print. CZPT gearboxes are available in a wide range of sizes and can produce high torque on the output axis.
High reduction ratio
Among the types of gearboxes available, a high reduction ratio cycloidal gearbox is a popular choice in the automation field. This gearbox is used in applications requiring precise output and high efficiency.
Cycloid gears can provide high torque and transmit it well. They have low friction and a small backlash. They are widely used in robotic joints. However, they require special tools to manufacture. Some have even been 3D printed.
A cycloidal gearbox is typically a three-stage structure that includes an input hub, an output hub, and two cycloidal gears that rotate around each other. The input hub mounts movable pins and rollers, while the output hub mounts a stationary ring gear.
The input shaft is driven by an eccentric bearing. The disc is then pushed against the ring gear, which causes it to rotate around the bearing. As the disc rotates, the pins on the ring gear drive the pins on the output shaft.
The input shaft rotates a maximum of nine revolutions, while the output shaft rotates three revolutions. This means that the input shaft has to rotate over eleven million times before the output shaft is able to rotate. The output shaft also rotates in the opposite direction of the input shaft.
In a two-stage differential cycloidal speed reducer, the input shaft uses a crank shaft design. The crank shaft connects the first and second cycloidal gears and actuates them simultaneously.
The first stage is a cycloidal disc, which is a gear tooth profile. It has n=7 lobes on its circumference. Each lobe moves around a reference pitch circle of pins. The disc then advances in 360deg steps.
The second stage is a cycloidal disc, also known as a “grinder gear”. The teeth on the outer gear are fewer than the teeth on the inner gear. This allows the gear to be geardown based on the number of teeth.
Kinematics
Various scholars have studied the kinematics of cycloidal gearbox. They have developed various approaches to modify the tooth profile of cycloidal gears. Some of these approaches involve changing the shape of the cycloidal disc, and changing the grinding wheel center position.
This paper describes a new approach to cycloid gear profile modification. It is based on a mathematical model and incorporates several important parameters such as pressure angle, backlash, and root clearance. The study offers a new way for modification design of cycloid gears in precision reducers for robots.
The pressure angle of a tooth profile is an intersegment angle between the normal direction and the velocity direction at a meshing point. The pressure angle distribution is important for determining force transmission performance of gear teeth in meshing. The distribution trend can be obtained by calculating the equation (5).
The mathematical model for modification of the tooth profile can be obtained by establishing the relationship between the pressure angle distribution and the modification function. The dependent variable is the modification DL and the independent variable is the pressure angle a.
The position of the reference point A is a major consideration in the modification design. It ensures the force transmission performance of the meshing segment is optimal. It is determined by the smallest profile pressure angle. The position is also dependent on the type of gear that is being modified. It is also influenced by the tooth backlash.
The mathematical model governing the pressure angle distribution is developed with DL=f(a). It is a piecewise function that determines the pressure angle distribution of a tooth profile. It can also be expressed as DL=ph.
The pressure angle of a tooth is also an angle between the common normal direction at the meshing point and the rotation velocity direction of the cycloid gear.
Planetary gearboxes vs cycloidal gearboxes
Generally, there are two types of gearboxes that are used for motion control applications: cycloidal gearbox and planetary gearbox. Cycloid gearboxes are used for high-frequency motions, while planetary gearboxes are suitable for low-speed applications. Both are highly accurate and precise gearboxes that are capable of handling heavy loads at high cycle rates. But they have different advantages and disadvantages. So, engineers need to determine which type of gearbox is best suited for their application.
Cycloid gearboxes are commonly used in industrial automation. They provide excellent performance with ratios as low as 10:1. They offer a more compact design, higher torque density and greater overload protection. They also require less space and are less expensive than planetary gearboxes.
On the other hand, planetary gearboxes are lightweight and offer a higher torque density. They are also capable of handling higher ratios. They have a longer life span and are more precise and durable. They can be found in a variety of styles, including square-framed, round-framed and double-frame designs. They offer a wide range of torque and speed capabilities and are used for numerous applications.
Cycloid gearboxes can be manufactured with different types of cycloidal cams, including single or compound cycloidal cams. Cycloid cams are cylindrical elements that have cam followers that rotate in an eccentric fashion. The cam followers act like teeth on the internal gear. Cycloid cams are a simple concept, but they have numerous advantages. They have a low backlash over extended periods of time, allowing for more accurate positioning. They also have internal compressive stresses and an overlap factor between the rolling elements.
Planetary gearboxes are characterized by three basic force-transmitting elements: ring gear, sun gear, and planet gear. They are generally two-stage gearboxes. The sun gear is attached to the input shaft, which in turn is attached to the servomotor. The ring gear turns the sun gear and the planet gear turns the output shaft.

editor by CX 2023-03-31
China Gpb090 Gvb Gpg Gear Box Gearbox High Precision Planetary Gearhead with Cheap Price supplier
Solution Description
TaiBang Motor Business Team Co., Ltd.
The major goods is induction motor, reversible motor, DC brush gear motor, DC brushless equipment motor, CH/CV huge gear motors, Planetary gear motor ,Worm equipment motor etc, which used widely in various fields of manufacturing pipelining, transportation, foodstuff, medication, printing, material, packing, office, equipment, entertainment and so on, and is the preferred and matched merchandise for automatic equipment.
Product Instruction
GB090-10-P2
| GB | 090 | 571 | P2 |
| Reducer Series Code | External Diameter | Reduction Ratio | Reducer Backlash |
| GB:High Precision Square Flange Output
GBR:Large Precision Right Angle Square Flange Output GE:Higher Precision Spherical Flange Output GER:Higher Precision Correct Round Flange Output |
050:ø50mm 070:ø70mm 090:ø90mm a hundred and twenty:ø120mm a hundred and fifty five:ø155mm 205:ø205mm 235:ø235mm 042:42x42mm 060:60x60mm 090:90x90mm a hundred and fifteen:115x115mm 142:142x142mm one hundred eighty:180x180mm 220:220x220mm |
571 indicates 1:ten | P0:Higher Precision Backlash
P1:Precision Backlash P2:Normal Backlash |
Major Technical Performance
| Merchandise | Amount of phase | Reduction Ratio | GB042 | GB060 | GB060A | GB090 | GB090A | GB115 | GB142 | GB180 | GB220 |
| Rotary Inertia | 1 | 3 | .03 | .16 | .61 | 3.25 | 9.21 | 28.98 | sixty nine.61 | ||
| 4 | .03 | .fourteen | .forty eight | 2.seventy four | 7.fifty four | 23.67 | 54.37 | ||||
| 5 | .03 | .13 | .forty seven | two.71 | seven.forty two | 23.29 | fifty three.27 | ||||
| six | .03 | .thirteen | .forty five | two.65 | seven.twenty five | 22.seventy five | fifty one.72 | ||||
| 7 | .03 | .thirteen | .45 | two.sixty two | 7.fourteen | 22.48 | fifty.ninety seven | ||||
| 8 | .03 | .13 | .44 | two.58 | 7.07 | 22.fifty nine | 50.84 | ||||
| 9 | .03 | .13 | .forty four | two.57 | 7.04 | 22.fifty three | 50.63 | ||||
| 10 | .03 | .13 | .forty four | 2.57 | seven.03 | 22.51 | fifty.56 | ||||
| 2 | fifteen | .03 | .03 | .13 | .13 | .47 | .47 | two.seventy one | 7.42 | 23.29 | |
| twenty | .03 | .03 | .13 | .thirteen | .47 | .47 | two.71 | 7.42 | 23.29 | ||
| twenty five | .03 | .03 | .thirteen | .13 | .forty seven | .47 | two.71 | seven.42 | 23.29 | ||
| thirty | .03 | .03 | .13 | .thirteen | .forty seven | .forty seven | 2.71 | 7.42 | 23.29 | ||
| 35 | .03 | .03 | .13 | .13 | .47 | .47 | two.71 | seven.forty two | 23.29 | ||
| 40 | .03 | .03 | .13 | .thirteen | .forty seven | .47 | two.71 | seven.42 | 23.29 | ||
| forty five | .03 | .03 | .13 | .13 | .47 | .47 | two.71 | seven.42 | 23.29 | ||
| 50 | .03 | .03 | .thirteen | .13 | .44 | .forty four | 2.57 | seven.03 | 22.51 | ||
| 60 | .03 | .03 | .thirteen | .13 | .44 | .44 | 2.fifty seven | 7.03 | 22.fifty one | ||
| 70 | .03 | .03 | .thirteen | .thirteen | .44 | .forty four | 2.fifty seven | 7.03 | 22.51 | ||
| 80 | .03 | .03 | .13 | .13 | .44 | .44 | two.fifty seven | seven.03 | 22.fifty one | ||
| 90 | .03 | .03 | .thirteen | .thirteen | .forty four | .forty four | two.57 | 7.03 | 22.fifty one | ||
| 100 | .03 | .03 | .13 | .13 | .44 | .44 | two.fifty seven | seven.03 | 22.fifty one |
| Item | Amount of stage | GB042 | GB060 | GB060A | GB90 | GB090A | GB115 | GB142 | GB180 | GB220 | |
| Backlash(arcmin) | High Precision P0 | 1 | ≤1 | ≤1 | ≤1 | ≤1 | ≤1 | ≤1 | |||
| 2 | ≤3 | ≤3 | ≤3 | ≤3 | |||||||
| Precision P1 | 1 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | |
| 2 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ||
| Standard P2 | 1 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | |
| 2 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ||
| Torsional Rigidity(N.M/arcmin) | one | three | seven | 7 | fourteen | fourteen | 25 | fifty | 145 | 225 | |
| 2 | three | 7 | seven | fourteen | 14 | 25 | 50 | a hundred forty five | 225 | ||
| Noise(dB) | one,2 | ≤56 | ≤58 | ≤58 | ≤60 | ≤60 | ≤63 | ≤65 | ≤67 | ≤70 | |
| Rated input speed(rpm) | 1,two | 5000 | 5000 | 5000 | 4000 | 4000 | 4000 | 3000 | 3000 | 2000 | |
| Max enter speed(rpm) | 1,two | ten thousand | 10000 | 10000 | 8000 | 8000 | 8000 | 6000 | 6000 | 4000 | |
Noise examination standard:Length 1m,no load.Measured with an input pace 3000rpm
|
US $50 / Piece | |
1 Piece (Min. Order) |
###
| Application: | Machinery, Agricultural Machinery |
|---|---|
| Function: | Distribution Power, Change Drive Torque, Change Drive Direction, Speed Reduction |
| Layout: | Cycloidal |
| Hardness: | Hardened Tooth Surface |
| Installation: | Vertical Type |
| Step: | Double-Step |
###
| Samples: |
US$ 50/Piece
1 Piece(Min.Order) |
|---|
###
| Customization: |
Available
|
|---|
###
| GB | 090 | 010 | P2 |
| Reducer Series Code | External Diameter | Reduction Ratio | Reducer Backlash |
| GB:High Precision Square Flange Output
GBR:High Precision Right Angle Square Flange Output GE:High Precision Round Flange Output GER:High Precision Right Round Flange Output |
050:ø50mm 070:ø70mm 090:ø90mm 120:ø120mm 155:ø155mm 205:ø205mm 235:ø235mm 042:42x42mm 060:60x60mm 090:90x90mm 115:115x115mm 142:142x142mm 180:180x180mm 220:220x220mm |
010 means 1:10 | P0:High Precision Backlash
P1:Precision Backlash P2:Standard Backlash |
###
| Item | Number of stage | Reduction Ratio | GB042 | GB060 | GB060A | GB090 | GB090A | GB115 | GB142 | GB180 | GB220 |
| Rotary Inertia | 1 | 3 | 0.03 | 0.16 | 0.61 | 3.25 | 9.21 | 28.98 | 69.61 | ||
| 4 | 0.03 | 0.14 | 0.48 | 2.74 | 7.54 | 23.67 | 54.37 | ||||
| 5 | 0.03 | 0.13 | 0.47 | 2.71 | 7.42 | 23.29 | 53.27 | ||||
| 6 | 0.03 | 0.13 | 0.45 | 2.65 | 7.25 | 22.75 | 51.72 | ||||
| 7 | 0.03 | 0.13 | 0.45 | 2.62 | 7.14 | 22.48 | 50.97 | ||||
| 8 | 0.03 | 0.13 | 0.44 | 2.58 | 7.07 | 22.59 | 50.84 | ||||
| 9 | 0.03 | 0.13 | 0.44 | 2.57 | 7.04 | 22.53 | 50.63 | ||||
| 10 | 0.03 | 0.13 | 0.44 | 2.57 | 7.03 | 22.51 | 50.56 | ||||
| 2 | 15 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | |
| 20 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 25 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 30 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 35 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 40 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 45 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 50 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 | ||
| 60 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 | ||
| 70 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 | ||
| 80 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 | ||
| 90 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 | ||
| 100 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 |
###
| Item | Number of stage | GB042 | GB060 | GB060A | GB90 | GB090A | GB115 | GB142 | GB180 | GB220 | |
| Backlash(arcmin) | High Precision P0 | 1 | ≤1 | ≤1 | ≤1 | ≤1 | ≤1 | ≤1 | |||
| 2 | ≤3 | ≤3 | ≤3 | ≤3 | |||||||
| Precision P1 | 1 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | |
| 2 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ||
| Standard P2 | 1 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | |
| 2 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ||
| Torsional Rigidity(N.M/arcmin) | 1 | 3 | 7 | 7 | 14 | 14 | 25 | 50 | 145 | 225 | |
| 2 | 3 | 7 | 7 | 14 | 14 | 25 | 50 | 145 | 225 | ||
| Noise(dB) | 1,2 | ≤56 | ≤58 | ≤58 | ≤60 | ≤60 | ≤63 | ≤65 | ≤67 | ≤70 | |
| Rated input speed(rpm) | 1,2 | 5000 | 5000 | 5000 | 4000 | 4000 | 4000 | 3000 | 3000 | 2000 | |
| Max input speed(rpm) | 1,2 | 10000 | 10000 | 10000 | 8000 | 8000 | 8000 | 6000 | 6000 | 4000 | |
|
US $50 / Piece | |
1 Piece (Min. Order) |
###
| Application: | Machinery, Agricultural Machinery |
|---|---|
| Function: | Distribution Power, Change Drive Torque, Change Drive Direction, Speed Reduction |
| Layout: | Cycloidal |
| Hardness: | Hardened Tooth Surface |
| Installation: | Vertical Type |
| Step: | Double-Step |
###
| Samples: |
US$ 50/Piece
1 Piece(Min.Order) |
|---|
###
| Customization: |
Available
|
|---|
###
| GB | 090 | 010 | P2 |
| Reducer Series Code | External Diameter | Reduction Ratio | Reducer Backlash |
| GB:High Precision Square Flange Output
GBR:High Precision Right Angle Square Flange Output GE:High Precision Round Flange Output GER:High Precision Right Round Flange Output |
050:ø50mm 070:ø70mm 090:ø90mm 120:ø120mm 155:ø155mm 205:ø205mm 235:ø235mm 042:42x42mm 060:60x60mm 090:90x90mm 115:115x115mm 142:142x142mm 180:180x180mm 220:220x220mm |
010 means 1:10 | P0:High Precision Backlash
P1:Precision Backlash P2:Standard Backlash |
###
| Item | Number of stage | Reduction Ratio | GB042 | GB060 | GB060A | GB090 | GB090A | GB115 | GB142 | GB180 | GB220 |
| Rotary Inertia | 1 | 3 | 0.03 | 0.16 | 0.61 | 3.25 | 9.21 | 28.98 | 69.61 | ||
| 4 | 0.03 | 0.14 | 0.48 | 2.74 | 7.54 | 23.67 | 54.37 | ||||
| 5 | 0.03 | 0.13 | 0.47 | 2.71 | 7.42 | 23.29 | 53.27 | ||||
| 6 | 0.03 | 0.13 | 0.45 | 2.65 | 7.25 | 22.75 | 51.72 | ||||
| 7 | 0.03 | 0.13 | 0.45 | 2.62 | 7.14 | 22.48 | 50.97 | ||||
| 8 | 0.03 | 0.13 | 0.44 | 2.58 | 7.07 | 22.59 | 50.84 | ||||
| 9 | 0.03 | 0.13 | 0.44 | 2.57 | 7.04 | 22.53 | 50.63 | ||||
| 10 | 0.03 | 0.13 | 0.44 | 2.57 | 7.03 | 22.51 | 50.56 | ||||
| 2 | 15 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | |
| 20 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 25 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 30 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 35 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 40 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 45 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 50 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 | ||
| 60 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 | ||
| 70 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 | ||
| 80 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 | ||
| 90 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 | ||
| 100 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 |
###
| Item | Number of stage | GB042 | GB060 | GB060A | GB90 | GB090A | GB115 | GB142 | GB180 | GB220 | |
| Backlash(arcmin) | High Precision P0 | 1 | ≤1 | ≤1 | ≤1 | ≤1 | ≤1 | ≤1 | |||
| 2 | ≤3 | ≤3 | ≤3 | ≤3 | |||||||
| Precision P1 | 1 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | |
| 2 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ||
| Standard P2 | 1 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | |
| 2 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ||
| Torsional Rigidity(N.M/arcmin) | 1 | 3 | 7 | 7 | 14 | 14 | 25 | 50 | 145 | 225 | |
| 2 | 3 | 7 | 7 | 14 | 14 | 25 | 50 | 145 | 225 | ||
| Noise(dB) | 1,2 | ≤56 | ≤58 | ≤58 | ≤60 | ≤60 | ≤63 | ≤65 | ≤67 | ≤70 | |
| Rated input speed(rpm) | 1,2 | 5000 | 5000 | 5000 | 4000 | 4000 | 4000 | 3000 | 3000 | 2000 | |
| Max input speed(rpm) | 1,2 | 10000 | 10000 | 10000 | 8000 | 8000 | 8000 | 6000 | 6000 | 4000 | |
Cyclone Gearbox Vs Involute Gearbox
Whether you’re using a cycloidal gearbox or an involute gearbox for your application, there are a few things you should know. This article will highlight some of those things, including: cycloidal gearbox vs involute gearbox, weight, compressive force, precision, and torque density.
Compressive force
Several studies have been carried out to analyze the static characteristics of gears. In this article, the authors investigate the structural and kinematic principles of a cycloidal gearbox. The cycloidal gearbox is a gearbox that uses an eccentric bearing inside a rotating frame. It has no common pinion-gear pair, and is therefore ideal for a high reduction ratio.
The purpose of this paper is to investigate the stress distribution on a cycloidal disc. Various gear profiles are investigated in order to study the load distribution and dynamic effects.
Cycloidal gearboxes are subject to compression and backlash, which require the use of proper ratios for the bearing rate and the TSA. The paper also focuses on the kinematic principles of the reducer. In addition, the authors use standard analysis techniques for the shaft/gear and the cycloidal disc.
The authors previously worked on a rigid body dynamic simulation of a cycloidal reducer. The analysis used a trochoidal profile on the cycloidal disc periphery. The trochoidal profile is obtained from a manufacturing drawing and takes into account the tolerances.
The mesh density in the cycloidal disc captures the exact geometry of the parts. It provides accurate contact stresses.
The cycloidal disc consists of nine lobes, which move by one lobe per rotation of the drive shaft. However, when the disc is rotated around the pins, the cycloidal disc does not move around the center of gravity. Therefore, the cycloidal disc shares torque load with five outer rollers.
A low reduction ratio in a cycloidal gearbox results in a higher induced stress in the cycloidal disc. This is due to the bigger hole designed to reduce the material inside the disc.
Torque density
Several types of magnetic gearboxes have been studied. Some magnetic gearboxes have a higher torque density than others, but they are still not able to compete with the mechanical gearboxes.
A new high torque density cycloidal magnetic gearbox using Halbach rotors has been developed and is being tested. The design was validated by building a CPCyMG prototype. The results showed that the simulated slip torque was comparable to the experimental slip torque. The peak torque measured was a p3 = 14 spatial harmonic, and it corresponds to the active region torque density of 261.4 N*m/L.
This cycloidal gearbox also has a high gear ratio. It has been tested to achieve a peak torque of 147.8 Nm, which is more than double the torque density of the traditional cycloidal gearbox. The design incorporates a ferromagnetic back-support that provides mechanical fabrication support.
This cycloidal gearbox also shows how a small diameter can achieve a high torque density. It is designed with an axial length of 50mm. The radial deflection forces are not serious at this length. The design uses a small air gap to reduce the radial deflection forces, but it is not the only design option.
The trade-off design also has a high volumetric torque density. It has a smaller air gap and a higher mass torque density. It is feasible to make and mechanically strong. The design is also one of the most efficient in its class.
The helical gearing design is a newer technology that brings a higher level of precision to a cycloidal gearbox. It allows a servomotor to handle a heavy load at high cycle rates. It is also useful in applications that require smaller design envelopes.
Weight
Compared to planetary gearboxes, the weight of cycloidal gearboxes is not as significant. However, they do provide some advantages. One of the most significant features is their backlash-free operation, which helps them deliver smooth and precise movement.
In addition, they provide high efficiency, which means that servo motors can run at higher speeds. The best part is that they do not need to be stacked up in order to achieve a high ratio.
Another advantage of cycloidal gearboxes is that they are usually less expensive than planetary gearboxes. This means that they are suitable for the manufacturing industry and robotics. They are also suited for heavy-duty robots that require a robust gearbox.
They also provide a better reduction ratio. Cycloidal gears can achieve reduction ratios from 30:1 to 300:1, which is a huge improvement over planetary gears. However, there are few models available that provide a ratio below 30:1.
Cycloidal gears also offer more resistance to wear, which means that they can last longer than planetary gears. They are also more compact, which helps them achieve high ratios in a smaller space. The design of cycloidal gears also makes them less prone to backlash, which is one of the major shortcomings of planetary gearboxes.
In addition, cycloidal gears can also provide better positioning accuracy. In fact, this is one of the primary reasons for choosing cycloidal gears over planetary gears. This is because the cycloid disc rotates around a bearing independently of the input shaft.
Compared to planetary gearboxes, cycloidal gears are also much shorter. This means that they provide the best positioning accuracy. They are also 50% lighter, meaning that they have a smaller diameter.
Precision
Several experts have studied the cycloidal gearbox in precision reducers. Their research mainly focuses on the mathematical model and the method for precision evaluation of cycloidal gears.
The traditional modification design of cycloidal gears is mainly realized by setting various machining parameters and center position of the grinding wheel. But it has some disadvantages because of unstable meshing accuracy and uncontrollable tooth profile curve shape.
In this study, a new method of modification design of cycloidal gears is proposed. This method is based on the calculation of meshing backlash and pressure angle distribution. It can effectively pre-control the transmission accuracy of cycloid-pin gear. It can also ensure good meshing characteristics.
The proposed method can be applied in the manufacture of rotary vector reducers. It is also applicable in the precision reducer for robots.
The mathematical model for cycloidal gears can be established with the pressure angle a as a dependent variable. It is possible to calculate the pressure angle distribution and the profile pressure angle. It can also be expressed as DL=f(a). It can be applied in the design of precision reducers.
The study also considers the root clearance, the backlash of gear teeth and the profile angle. These factors have a direct effect on the transmission performance of cycloidal gear. It also indicates the higher motion accuracy and the smaller backlash. The modified profile can also reflect the smaller transmission error.
In addition, the proposed method is also based on the calculation of lost motion. It determines the angle of first tooth contacts. This angle is an important factor affecting the modification quality. The transmission error after the second cycloid method is the least.
Finally, a case study on the CZPT RV-35N gear pair is shown to prove the proposed method.
Involute gears vs cycloidal gears
Compared to involute gears, cycloidal gears have a lower noise, less friction, and last longer. However, they are more expensive. Cycloidal gears can be more difficult to manufacture. They may be less suitable for certain applications, including space manipulators and robotic joints.
The most common gear profile is the involute curve of a circle. This curve is formed by the endpoint of an imaginary taut string unwinding from the circle.
Another curve is the epicycloid curve. This curve is formed by the point rigidly attached to the circle rolling over another circle. This curve is difficult to produce and is much more expensive to produce than the involute curve.
The cycloid curve of a circle is also an example of the multi-cursor. This curve is generated by the locus of the point on the circle’s circumference.
The cycloid curve has the same diameter as the involute curve, but is tangentially curving along the circle’s diameter. This curve is also classified as ordinary. It has several other functions. The FE method was used to analyze the strain state of cycloidal speed reducers.
There are many other curves, but the involute curve is the most widely used gear profile. The involute curve of a circle is a spiraling curve traced by the endpoint of an imaginary tautstring.
Involute gears are a lot like a set of Lego blocks. They are a lot of fun to play with. They also have a lot of advantages. For example, they can handle center sifts better than cycloidal gears. They are also much easier to manufacture, so the cost of involute teeth is lower. However, they are obsolete.
Cycloidal gears are also more difficult to manufacture than involute gears. They have a convex surface, which leads to more wear. They also have a simpler shape than involute gears. They also have less teeth. They are used in rotary motions, such as in the rotors of screw compressors.

editor by czh 2023-01-05
China Factory Gear Box Gpb Gpg Servo Motor Gearhead High Precision Planetary Gearbox for Woodworking Machinery cycloidal gearbox lubrication
Merchandise Description
TaiBang Motor Business Group Co., Ltd.
The major products is induction motor, reversible motor, DC brush equipment motor, DC brushless equipment motor, CH/CV huge equipment motors, Planetary gear motor ,Worm equipment motor etc, which utilized extensively in a variety of fields of producing pipelining, transportation, foods, medication, printing, cloth, packing, place of work, equipment, enjoyment and so on, and is the desired and matched merchandise for computerized device.
Product Instruction
GB090-ten-P2
| GB | 090 | 571 | P2 |
| Reducer Collection Code | External Diameter | Reduction Ratio | Reducer Backlash |
| GB:Substantial Precision Square Flange Output
GBR:Large Precision Appropriate Angle Square Flange Output GE:Large Precision Spherical Flange Output GER:High Precision Correct Spherical Flange Output |
050:ø50mm 070:ø70mm 090:ø90mm a hundred and twenty:ø120mm 155:ø155mm 205:ø205mm 235:ø235mm 042:42x42mm 060:60x60mm 090:90x90mm one hundred fifteen:115x115mm 142:142x142mm 180:180x180mm 220:220x220mm |
571 means 1:ten | P0:Large Precision Backlash
P1:Precison Backlash P2:Normal Backlash |
Primary Complex Overall performance
| Merchandise | Variety of phase | Reduction Ratio | GB042 | GB060 | GB060A | GB090 | GB090A | GB115 | GB142 | GB180 | GB220 |
| Rotary Inertia | 1 | 3 | .03 | .16 | .61 | 3.25 | nine.21 | 28.ninety eight | 69.61 | ||
| four | .03 | .14 | .48 | two.74 | seven.54 | 23.sixty seven | fifty four.37 | ||||
| five | .03 | .13 | .forty seven | 2.seventy one | seven.forty two | 23.29 | fifty three.27 | ||||
| six | .03 | .thirteen | .45 | two.65 | 7.twenty five | 22.seventy five | 51.72 | ||||
| seven | .03 | .thirteen | .forty five | two.62 | 7.14 | 22.48 | 50.97 | ||||
| eight | .03 | .13 | .44 | two.58 | seven.07 | 22.59 | 50.84 | ||||
| nine | .03 | .13 | .44 | two.fifty seven | seven.04 | 22.fifty three | fifty.63 | ||||
| 10 | .03 | .13 | .44 | two.57 | seven.03 | 22.fifty one | fifty.56 | ||||
| 2 | 15 | .03 | .03 | .thirteen | .13 | .47 | .47 | 2.71 | 7.42 | 23.29 | |
| twenty | .03 | .03 | .13 | .thirteen | .47 | .47 | two.seventy one | 7.forty two | 23.29 | ||
| 25 | .03 | .03 | .thirteen | .13 | .47 | .47 | 2.seventy one | seven.42 | 23.29 | ||
| 30 | .03 | .03 | .thirteen | .13 | .forty seven | .47 | 2.seventy one | seven.42 | 23.29 | ||
| 35 | .03 | .03 | .13 | .13 | .forty seven | .forty seven | two.seventy one | 7.42 | 23.29 | ||
| forty | .03 | .03 | .thirteen | .13 | .forty seven | .forty seven | two.seventy one | 7.forty two | 23.29 | ||
| 45 | .03 | .03 | .13 | .13 | .47 | .47 | 2.seventy one | 7.forty two | 23.29 | ||
| fifty | .03 | .03 | .thirteen | .13 | .forty four | .forty four | 2.fifty seven | seven.03 | 22.fifty one | ||
| 60 | .03 | .03 | .thirteen | .thirteen | .44 | .44 | 2.fifty seven | seven.03 | 22.51 | ||
| 70 | .03 | .03 | .thirteen | .thirteen | .forty four | .forty four | 2.fifty seven | seven.03 | 22.fifty one | ||
| 80 | .03 | .03 | .13 | .13 | .44 | .forty four | two.fifty seven | seven.03 | 22.fifty one | ||
| ninety | .03 | .03 | .13 | .thirteen | .forty four | .forty four | two.fifty seven | 7.03 | 22.51 | ||
| a hundred | .03 | .03 | .13 | .thirteen | .forty four | .44 | two.57 | seven.03 | 22.51 |
| Item | Number of stage | GB042 | GB060 | GB060A | GB90 | GB090A | GB115 | GB142 | GB180 | GB220 | |
| Backlash(arcmin) | High Precision P0 | one | ≤1 | ≤1 | ≤1 | ≤1 | ≤1 | ≤1 | |||
| 2 | ≤3 | ≤3 | ≤3 | ≤3 | |||||||
| Precision P1 | one | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | |
| two | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ||
| Standard P2 | one | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | |
| two | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ||
| Torsional Rigidity(N.M/arcmin) | 1 | three | seven | seven | 14 | 14 | twenty five | fifty | a hundred forty five | 225 | |
| two | three | seven | seven | 14 | 14 | 25 | 50 | 145 | 225 | ||
| Noise(dB) | 1,2 | ≤56 | ≤58 | ≤58 | ≤60 | ≤60 | ≤63 | ≤65 | ≤67 | ≤70 | |
| Rated enter velocity(rpm) | one,two | 5000 | 5000 | 5000 | 4000 | 4000 | 4000 | 3000 | 3000 | 2000 | |
| Max enter velocity(rpm) | one,2 | 10000 | 10000 | 10000 | 8000 | 8000 | 8000 | 6000 | 6000 | 4000 | |
Noise check regular:Length 1m,no load.Calculated with an enter speed 3000rpm
|
US $50 / Piece | |
1 Piece (Min. Order) |
###
| Application: | Machinery, Agricultural Machinery |
|---|---|
| Function: | Distribution Power, Change Drive Torque, Change Drive Direction, Speed Reduction |
| Layout: | Cycloidal |
| Hardness: | Hardened Tooth Surface |
| Installation: | Vertical Type |
| Step: | Double-Step |
###
| Samples: |
US$ 50/Piece
1 Piece(Min.Order) |
|---|
###
| Customization: |
Available
|
|---|
###
| GB | 090 | 010 | P2 |
| Reducer Series Code | External Diameter | Reduction Ratio | Reducer Backlash |
| GB:High Precision Square Flange Output
GBR:High Precision Right Angle Square Flange Output GE:High Precision Round Flange Output GER:High Precision Right Round Flange Output |
050:ø50mm 070:ø70mm 090:ø90mm 120:ø120mm 155:ø155mm 205:ø205mm 235:ø235mm 042:42x42mm 060:60x60mm 090:90x90mm 115:115x115mm 142:142x142mm 180:180x180mm 220:220x220mm |
010 means 1:10 | P0:High Precision Backlash
P1:Precison Backlash P2:Standard Backlash |
###
| Item | Number of stage | Reduction Ratio | GB042 | GB060 | GB060A | GB090 | GB090A | GB115 | GB142 | GB180 | GB220 |
| Rotary Inertia | 1 | 3 | 0.03 | 0.16 | 0.61 | 3.25 | 9.21 | 28.98 | 69.61 | ||
| 4 | 0.03 | 0.14 | 0.48 | 2.74 | 7.54 | 23.67 | 54.37 | ||||
| 5 | 0.03 | 0.13 | 0.47 | 2.71 | 7.42 | 23.29 | 53.27 | ||||
| 6 | 0.03 | 0.13 | 0.45 | 2.65 | 7.25 | 22.75 | 51.72 | ||||
| 7 | 0.03 | 0.13 | 0.45 | 2.62 | 7.14 | 22.48 | 50.97 | ||||
| 8 | 0.03 | 0.13 | 0.44 | 2.58 | 7.07 | 22.59 | 50.84 | ||||
| 9 | 0.03 | 0.13 | 0.44 | 2.57 | 7.04 | 22.53 | 50.63 | ||||
| 10 | 0.03 | 0.13 | 0.44 | 2.57 | 7.03 | 22.51 | 50.56 | ||||
| 2 | 15 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | |
| 20 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 25 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 30 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 35 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 40 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 45 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 50 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 | ||
| 60 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 | ||
| 70 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 | ||
| 80 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 | ||
| 90 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 | ||
| 100 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 |
###
| Item | Number of stage | GB042 | GB060 | GB060A | GB90 | GB090A | GB115 | GB142 | GB180 | GB220 | |
| Backlash(arcmin) | High Precision P0 | 1 | ≤1 | ≤1 | ≤1 | ≤1 | ≤1 | ≤1 | |||
| 2 | ≤3 | ≤3 | ≤3 | ≤3 | |||||||
| Precision P1 | 1 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | |
| 2 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ||
| Standard P2 | 1 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | |
| 2 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ||
| Torsional Rigidity(N.M/arcmin) | 1 | 3 | 7 | 7 | 14 | 14 | 25 | 50 | 145 | 225 | |
| 2 | 3 | 7 | 7 | 14 | 14 | 25 | 50 | 145 | 225 | ||
| Noise(dB) | 1,2 | ≤56 | ≤58 | ≤58 | ≤60 | ≤60 | ≤63 | ≤65 | ≤67 | ≤70 | |
| Rated input speed(rpm) | 1,2 | 5000 | 5000 | 5000 | 4000 | 4000 | 4000 | 3000 | 3000 | 2000 | |
| Max input speed(rpm) | 1,2 | 10000 | 10000 | 10000 | 8000 | 8000 | 8000 | 6000 | 6000 | 4000 | |
|
US $50 / Piece | |
1 Piece (Min. Order) |
###
| Application: | Machinery, Agricultural Machinery |
|---|---|
| Function: | Distribution Power, Change Drive Torque, Change Drive Direction, Speed Reduction |
| Layout: | Cycloidal |
| Hardness: | Hardened Tooth Surface |
| Installation: | Vertical Type |
| Step: | Double-Step |
###
| Samples: |
US$ 50/Piece
1 Piece(Min.Order) |
|---|
###
| Customization: |
Available
|
|---|
###
| GB | 090 | 010 | P2 |
| Reducer Series Code | External Diameter | Reduction Ratio | Reducer Backlash |
| GB:High Precision Square Flange Output
GBR:High Precision Right Angle Square Flange Output GE:High Precision Round Flange Output GER:High Precision Right Round Flange Output |
050:ø50mm 070:ø70mm 090:ø90mm 120:ø120mm 155:ø155mm 205:ø205mm 235:ø235mm 042:42x42mm 060:60x60mm 090:90x90mm 115:115x115mm 142:142x142mm 180:180x180mm 220:220x220mm |
010 means 1:10 | P0:High Precision Backlash
P1:Precison Backlash P2:Standard Backlash |
###
| Item | Number of stage | Reduction Ratio | GB042 | GB060 | GB060A | GB090 | GB090A | GB115 | GB142 | GB180 | GB220 |
| Rotary Inertia | 1 | 3 | 0.03 | 0.16 | 0.61 | 3.25 | 9.21 | 28.98 | 69.61 | ||
| 4 | 0.03 | 0.14 | 0.48 | 2.74 | 7.54 | 23.67 | 54.37 | ||||
| 5 | 0.03 | 0.13 | 0.47 | 2.71 | 7.42 | 23.29 | 53.27 | ||||
| 6 | 0.03 | 0.13 | 0.45 | 2.65 | 7.25 | 22.75 | 51.72 | ||||
| 7 | 0.03 | 0.13 | 0.45 | 2.62 | 7.14 | 22.48 | 50.97 | ||||
| 8 | 0.03 | 0.13 | 0.44 | 2.58 | 7.07 | 22.59 | 50.84 | ||||
| 9 | 0.03 | 0.13 | 0.44 | 2.57 | 7.04 | 22.53 | 50.63 | ||||
| 10 | 0.03 | 0.13 | 0.44 | 2.57 | 7.03 | 22.51 | 50.56 | ||||
| 2 | 15 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | |
| 20 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 25 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 30 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 35 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 40 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 45 | 0.03 | 0.03 | 0.13 | 0.13 | 0.47 | 0.47 | 2.71 | 7.42 | 23.29 | ||
| 50 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 | ||
| 60 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 | ||
| 70 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 | ||
| 80 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 | ||
| 90 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 | ||
| 100 | 0.03 | 0.03 | 0.13 | 0.13 | 0.44 | 0.44 | 2.57 | 7.03 | 22.51 |
###
| Item | Number of stage | GB042 | GB060 | GB060A | GB90 | GB090A | GB115 | GB142 | GB180 | GB220 | |
| Backlash(arcmin) | High Precision P0 | 1 | ≤1 | ≤1 | ≤1 | ≤1 | ≤1 | ≤1 | |||
| 2 | ≤3 | ≤3 | ≤3 | ≤3 | |||||||
| Precision P1 | 1 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | ≤3 | |
| 2 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ||
| Standard P2 | 1 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | ≤5 | |
| 2 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ≤7 | ||
| Torsional Rigidity(N.M/arcmin) | 1 | 3 | 7 | 7 | 14 | 14 | 25 | 50 | 145 | 225 | |
| 2 | 3 | 7 | 7 | 14 | 14 | 25 | 50 | 145 | 225 | ||
| Noise(dB) | 1,2 | ≤56 | ≤58 | ≤58 | ≤60 | ≤60 | ≤63 | ≤65 | ≤67 | ≤70 | |
| Rated input speed(rpm) | 1,2 | 5000 | 5000 | 5000 | 4000 | 4000 | 4000 | 3000 | 3000 | 2000 | |
| Max input speed(rpm) | 1,2 | 10000 | 10000 | 10000 | 8000 | 8000 | 8000 | 6000 | 6000 | 4000 | |
How to Calculate Transmission Ratio for a Cycloidal Gearbox
Using a cycloidal gearbox can be very useful in a wide variety of situations. However, it’s important to understand how to use it properly before implementing it. This article discusses the benefits of using a cycloidal gearbox, how to calculate the transmission ratio, and how to determine the effects of dynamic and inertial forces on the gearbox.
Dynamic and inertial effects
Various studies have been done to study the dynamic and inertial effects of cycloidal gearboxes. These studies have been performed using numerical, analytical and experimental methods. Depending on the nature of the load and its distribution along the gear, a variety of models have been developed. These models use finite element method to determine accurate contact stresses. Some of these models have been developed to address the nonlinear elasticity of contacts.
Inertial imbalance in a cycloidal gearbox causes vibration and can affect the efficiency of the device. This can increase mechanical losses and increase wear and tear. The efficiency of the device also depends on the torque applied to the cycloidal disk. The effectiveness of the device increases as the load increases. Similarly, the nonlinear contact dynamics are also associated with an increase in efficiency.
A new model of a cycloidal reducer has been developed to predict the effects of several operational conditions. The model is based on rigid body dynamics and uses a non-linear stiffness coefficient. The model has been validated through numerical and analytical methods. The model offers drastic reduction in computational costs. The model allows for a quick analysis of several operational conditions.
The main contribution of the paper is the investigation of the load distribution on the cycloidal disc. The study of this aspect is important because it allows for an analysis of the rotating parts and stresses. It also provides an indication of which gear profiles are best suited for optimizing torque transmission. The study has been conducted with a variety of cycloidal gearboxes and is useful in determining the performance of different types of cycloidal gearboxes.
To study the load distribution on the cycloidal disc, the authors investigated the relationship between contact force, cycloidal gearboxes and different gear profiles. They found that the non-linear contact dynamics have a large impact on the efficiency of a cycloidal gearbox. The cycloidal gearbox is an ideal solution for applications that involve highly dynamic servos. It can also be used in machine tool applications and food processing industries.
The study found that there are three common design principles of cycloidal reducers. These are the contact force distribution, the speed reduction and the trochoidal profile of the cycloidal disc. The trochoidal profile has to be defined carefully to ensure correct mating of the rotating parts. The trochoidal profile provides an indication of which gear profiles are best for optimizing torque transmission. The contact force distribution can be improved by refining the mesh along the disc’s width.
As the input speed increases, the efficiency of the reducer increases. This is because contact forces are constantly changing in magnitude and orientation. A cycloidal reducer with a one tooth difference can reduce input speed by up to 87:1 in a single stage. It also has the ability to handle high-cycle moves without backlash.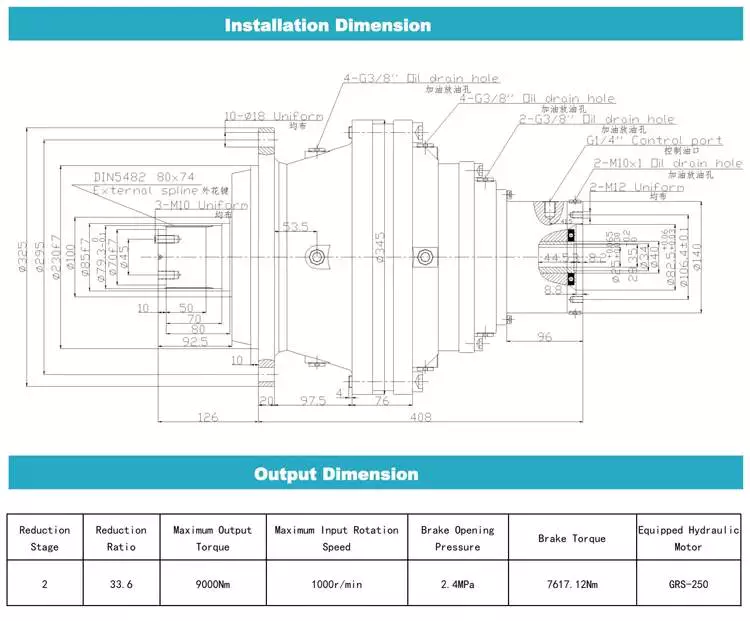
Transmission ratio calculation
Getting the correct transmission ratio calculation for a cycloidal gearbox requires a good understanding of what a gearbox is, as well as the product that it is being used for. The correct ratio is calculated by dividing the output speed of the output gear by the input speed of the input gear. This is usually accomplished by using a stopwatch. In some cases, a catalog or product specification may be required. The correct ratio is determined by a combination of factors, such as the amount of torque applied to the mechanism, as well as the size of the gears involved.
A cycloidal gear is a type of gear tooth profile that can be represented using a spline. It is also possible to model a gear with a cycloidal profile by using a spline to connect points against the beginning of a coordinate system. This is important in the design and functionality of a gear.
There are many different gears used in machines and devices. These include the herringbone gear, the helical gear and the spiral bevel gear. The best transmission ratios are typically obtained with a cycloidal gearbox. In addition to ensuring the accuracy of positioning, a cycloidal gearbox provides excellent backlash. Cycloid gears have a high degree of mechanical efficiency, low friction, and minimal moment of inertia.
A cycloidal gearbox is often referred to as a planetary gearbox, though it is technically a single-stage gearbox. In addition to having a ring gear, the gearbox has an eccentric bearing that drives the cycloidal disc in an eccentric rotation. This makes the cycloidal gearbox a good choice for high gear ratios in compact designs.
The cycloid disc is the key element of a cycloidal gearbox. The cycloid disc has n=9 lobes, and each lobe of the disc moves by a lobe for every revolution of the drive shaft. The cycloid disc is then geared to a stationary ring gear. The cycloidal disc’s lobes act like teeth on the stationary ring gear.
There are many different gears that are classified by the profile of the gear teeth. The most common gears are the involute and helical gears. Most motion control gears include spur designs. However, there are many other types of gears that are used in various applications. The cycloidal gear is one of the more complicated gears to design. The cycloid disc’s outline can be represented using markers or smooth lines, though a scatter chart will also do.
The cycloid disc’s lobes rotate on a reference pitch circle of pins. These pins rotate 40 deg during the eccentric rotation of the drive shaft. The pins rotate around the disc to achieve a steady rotation of the output shaft.
The cycloid disc’s other obvious, and possibly more important, feature is the’magic’ number of pins. This is the number of pins that protrude through the face of the disc. The disc has holes that are larger than the pins. This allows the pins to protrude through the disc and attach to the output shaft.
Application
Whether you’re building a robot drive or you’re simply looking for a gearbox to reduce the speed of your vehicle, a cycloidal gearbox is a great way to achieve a high reduction ratio. Cycloidal gearboxes are a low-friction, lightweight design that has an extremely stable transmission. They are suitable for industrial robots and can be used in many applications, including positioning robots.
Cycloidal gearboxes reduce speed by using eccentric motion. The eccentric motion enables the entire internal gear to rotate in wobbly cycloidal motion, which is then translated back into circular rotation. This eliminates the need for stacking gear stages. Cycloidal gearboxes also have less friction, higher strength, and greater durability than conventional gearboxes.
The cycloidal gearbox is also used in a number of applications, including marine propulsion systems, and robot drives. Cycloidal gearboxes reduce vibration by using offset gearing to cancel out vibrations.
Cycloidal gears have lower friction, higher strength, and better torsional stiffness than involute gears. They also have a reduced Hertzian contact stress, making them better than involute gears for use with shock loads. They also have a smaller size and weight than conventional gearboxes, and they have a higher reduction ratio than involute gears.
Cycloidal gears are typically used to reduce the speed of motors, but they also offer a number of other advantages. Cycloidal gearboxes have a smaller footprint than other gearboxes, allowing them to fit into confined spaces. They also have low backlash, allowing for precise movement. Cycloidal gears have a higher efficiency, resulting in lower power requirements and lower wear.
The cycloidal disc is one of the most important components of the gearbox. Cycloidal discs are normally designed with a short cycloid, which minimizes the eccentricity of the disc. They are also designed with a shortened flank, resulting in better strength and less stress concentration. Cycloidal discs are typically geared to a stationary ring gear. The cycloid is designed to roll around the stationary ring pins, which push against the circular holes in the disc. Cycloidal gearboxes typically employ two degrees of shift.
Cycloidal drives are ideal for heavy load applications. They also have high torsional stiffness, which makes them highly resistant to shock loads. Cycloidal drives also offer a high reduction ratio, which can be achieved without the need for a large input shaft. They are also compact and have a high service life.
The output shaft of a cycloidal gearbox always has two degrees of shifting, which ensures that the input and output shafts always rotate at a different speed. The output shaft would be a pin casing around the drive disks, which would also allow for easy maintenance.
Cycloidal gearboxes are also very compact and lightweight, so they are ideal for use in industrial robots. The cycloidal gearbox reducer is the most stable, low-vibration reducer in industrial robots, and it has a wide transmission ratio range.

editor by czh 2022-12-21